 por [icaro] » Dom Abr 17, 2011 12:44
por [icaro] » Dom Abr 17, 2011 12:44
A lei
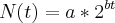
representa o crescimento de uma pop de bacterias. Neste caso, N(t) é o numero de bacterias no instante t (com t em horas) e a e b são constantes reais. Sabendo-se que no inicio da observação havia 3000 bacterias e que apos duas horas havia 4800 bacterias, determine:
a) os valores das constantes a e b
b) o numero de bacterias existentes apos meia hora
c) o tempo minimo necessario para que o numero de bacterias seja maior que 3 milhões
-
[icaro]
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Mar 09, 2011 00:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciências e tecnologia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4072 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5745 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- [função exponencial] Exprimir em função de x
por fff » Ter Jan 07, 2014 12:02
- 2 Respostas
- 3126 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 13:23
Funções
-
- funçao exponencial ITA
por zeramalho2004 » Dom Jun 28, 2009 19:55
- 3 Respostas
- 5118 Exibições
- Última mensagem por Marcampucio

Seg Jun 29, 2009 15:23
Funções
-
- Função Exponencial
por Aline » Seg Jun 29, 2009 18:59
- 3 Respostas
- 5901 Exibições
- Última mensagem por Cleyson007

Qua Jul 01, 2009 22:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
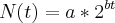 representa o crescimento de uma pop de bacterias. Neste caso, N(t) é o numero de bacterias no instante t (com t em horas) e a e b são constantes reais. Sabendo-se que no inicio da observação havia 3000 bacterias e que apos duas horas havia 4800 bacterias, determine:
representa o crescimento de uma pop de bacterias. Neste caso, N(t) é o numero de bacterias no instante t (com t em horas) e a e b são constantes reais. Sabendo-se que no inicio da observação havia 3000 bacterias e que apos duas horas havia 4800 bacterias, determine:

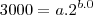
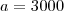
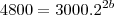
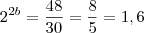
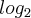 dos dois lados temos,
dos dois lados temos,

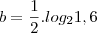
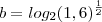
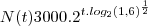
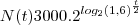

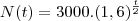


 .
.



