 por brunnomaia » Dom Mar 06, 2011 11:07
por brunnomaia » Dom Mar 06, 2011 11:07
Pessoal sou novo no fórum e este é meu primeiro tópico, desculpe se o tópico estiver no local errado.
Eu tenho 32 anos e estou querendo depois de velho tentar vestibular para Engenharia Civil, O fato é que estou com algumas apostilas de cursinho fazendo exercícios e esbarrei logo de cara na questão abaixo:
O fato é que a anos eu não vejo matemática então não sei nem por onde começar..
Eu tenho o resultado porém não consigo chegar nele, até imagino que seja bem simples mas minha cabeça não consegue puxar pela memória o que aprendi a anos atrás.
- Anexos
-
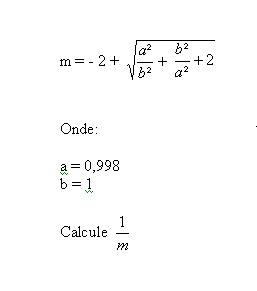
- Equação.JPG (5.77 KiB) Exibido 1810 vezes
-
brunnomaia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 06, 2011 10:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Dom Mar 06, 2011 11:40
por LuizAquino » Dom Mar 06, 2011 11:40
Você quer calcular

.
Portanto, você quer o valor de
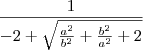
.
Primeiro, vamos simplificar um pouco essa raiz.
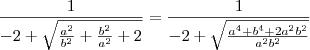
Usando o produto notável
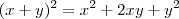
, nós temos que:
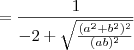
Como
a e
b são números positivos, podemos efetuar a simplificação entre a raiz quadrada e a potência 2.
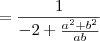
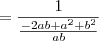
Usando o produto notável
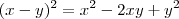
, temos que:

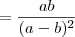
Agora, basta substituir os valores para
a e
b:
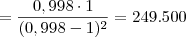 Sugestão
SugestãoAcredito que o tópico a seguir deva lhe interessar:
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por brunnomaia » Dom Mar 06, 2011 11:53
por brunnomaia » Dom Mar 06, 2011 11:53
Muito Obrigado!
Eu estava tentando simplificar desde o começo substituindo o b por 1 , não lembrava dos produtos notáveis!
-
brunnomaia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 06, 2011 10:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida - resolução função !
 por jamiel » Qui Mai 26, 2011 18:07
por jamiel » Qui Mai 26, 2011 18:07
- 11 Respostas
- 5930 Exibições
- Última mensagem por jamiel

Qui Mai 26, 2011 22:31
Funções
-
- Função Sen - Dúvida Resolução
por jamiel » Sáb Jul 02, 2011 17:47
- 7 Respostas
- 4481 Exibições
- Última mensagem por jamiel

Sáb Jul 02, 2011 19:42
Funções
-
- Função Exponencial - Dúvida na resolução!
por jamiel » Dom Mai 15, 2011 14:09
- 1 Respostas
- 4775 Exibições
- Última mensagem por Claudin

Dom Mai 15, 2011 14:21
Funções
-
- Retângulo - função(resolução-dúvida)
por jamiel » Seg Mai 23, 2011 14:44
- 2 Respostas
- 4030 Exibições
- Última mensagem por jamiel

Seg Mai 23, 2011 21:39
Funções
-
- Dúvida - resolução(função inversa)
por jamiel » Ter Jun 14, 2011 18:49
- 1 Respostas
- 1471 Exibições
- Última mensagem por DanielFerreira

Qui Jun 16, 2011 16:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.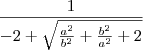 .
.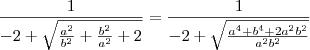
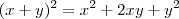 , nós temos que:
, nós temos que: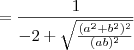
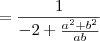
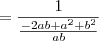
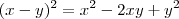 , temos que:
, temos que:
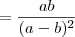
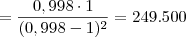


 .
.



