 por helenasilva » Qua Jan 26, 2011 07:45
por helenasilva » Qua Jan 26, 2011 07:45
Outra questão é a seguinte:
O que se prentende num exercicio que pede para caracterizar as funções??
aparece : Considera as funções reais de variável f(x)=x^2-1 e g(x)=1/x caracteriza as funções:
a) f+g
b) f x g
c) f/g
Não entendo que se pretende com caracteriza as funções!! Na 1ª chegei ate (f+g)= (x^3-x+1)/x agora não sei como caracterizar las podem me ajudar?? URGENTEMENTE..
-
helenasilva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 24, 2011 17:57
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Qua Jan 26, 2011 15:13
por Molina » Qua Jan 26, 2011 15:13
Boa tarde.
Tem alguma coisa a ver com o assunto que você está estudando de funções.
Talvez se são injetivas, sobrejetivas ou bijetivas..
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Qua Jan 26, 2011 15:47
por LuizAquino » Qua Jan 26, 2011 15:47
Olá Pessoal,
Dependendo do contexto, "caracterizar a função" pode significar você indicar a sua lei de formação. Por exemplo, considerando que
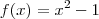
e
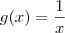
, temos que a caracterização de f+g será
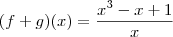
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por helenasilva » Qua Jan 26, 2011 18:20
por helenasilva » Qua Jan 26, 2011 18:20
Entao na alínea b) ficaria: (f×g)=(x^2-1)(1/x)
(f×g)= x^2+x^3-1-x ??
É só isso que é caracterizar?
-
helenasilva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 24, 2011 17:57
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por LuizAquino » Qua Jan 26, 2011 19:33
por LuizAquino » Qua Jan 26, 2011 19:33
Acredito que sim. Entretanto, note que se
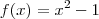
e
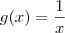
, então:
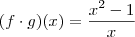
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por helenasilva » Qui Jan 27, 2011 18:51
por helenasilva » Qui Jan 27, 2011 18:51
ok obrigado pela resposta e agora percebo melhor o que e caracterizar funções..
-
helenasilva
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Jan 24, 2011 17:57
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3428 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4193 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3138 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3387 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2996 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



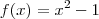 e
e 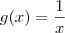 , temos que a caracterização de f+g será
, temos que a caracterização de f+g será 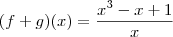 .
.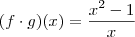

 .
.



