Ajuda com essa função

por **andreagenor** » Qui Nov 11, 2010 03:11

Olá eu estou desenvolvendo um aplicativo onde eu preciso obter o ângulo de visão de uma camera sendo que tenho o valor do comprimento de lente e da largura do filme.
Para isso eu estou usando a seguinte fórmula:
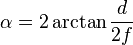
$Imagem$

Porem eu também preciso fazer ao contrário.
Saber o valor do comprimento da Lente (f), quando eu tiver apenas os outros valores ângulo de visão e largura do filme.

Eu tentei da seguinte forma, mas os resultados não deram certo.

f=d / 2 * tan(?/2)
Isso é uma tentativa de isolar o f da formula acima.

Alguém poderia me ajudar a fazer essa fórmula de forma correta e me explicar o procedimento?

por **MarceloFantini** » Qui Nov 11, 2010 03:46

por **andreagenor** » Qui Nov 11, 2010 16:09

só mais uma dúvida o resultado f será em radianos ou em graus?
Porque tem algo dando errado :(

Veja o que acontece ou se estou fazendo errado.

d= 36
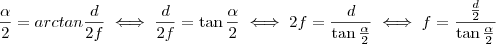
$\alpha$ = 39.6
o resultado de f deveria ser = 49.9969
Mas não da isso.