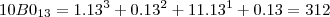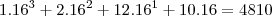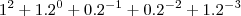por 91disakai » Qua Set 26, 2012 11:26
por 91disakai » Qua Set 26, 2012 11:26
bom dia !
Fellas preciso de uma grande ajuda de vocês !!
Tenho um prova quinta feira de Logica e Rselução de problemas, o professor passou alguns exercicios para estudo mas estou com muita duvida em relação a sistema de numeração:
1. No sistema de numeração de base 6:
1.1. Quantos símbolos (numerais) serão usados?
1.2. Quais numerais que já são utilizados no sistema de numeração decimal, serão utilizados?
1.3. O numeral 2, na primeira ordem, representa que quantidade numérica:
1.4. O numeral 3, na terceira ordem, representa que quantidade numérica;
1.5. Escreva 3526 como uma soma de potência de base 6:
1.6. Qual é a quantidade representada?
(NAO ESTOU CONSEGUINDO FAZER ESTAS QUESTOES !) PEÇO A AJUDA DE VOCES !!
-
91disakai
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Set 26, 2012 11:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: redes de computadores
- Andamento: cursando
 por young_jedi » Qua Set 26, 2012 12:05
por young_jedi » Qua Set 26, 2012 12:05
1-em um sistema de base seis
são utilizados 6 simbolos
2-voce pode utilizar 0,1,2,3,4,5
3-o numeral dois na primeira ordem representa 2 mesmo
4-o numeral 3 na terceira posição significa o numero
300
ou seja

5-o numero deve ser do tipo
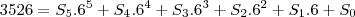
se eu dividir a equação por 6 o resto da divisão dara o numero
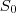
e um quociente.
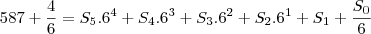
logo

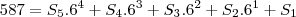
repetindo o processo eu encontro


então
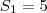

repetindo o processo voce encontrara os demais numeros
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por 91disakai » Qua Set 26, 2012 12:35
por 91disakai » Qua Set 26, 2012 12:35
Muito Obrigado!
Mas fiquei ainda com uma duvida:
Por exemo : 1.4. O numeral 3, na terceira ordem, representa que quantidade numérica; (se fosse na quarta ordem o numero 3 ia ser igual a 3.000? e outra coisa 1.5. Escreva 352(6) como uma soma de potência de base 6:
1.6. Qual é a quantidade representada?
ESSE DUAS eu ainda nao entendei poderia me explicar melhor ?
Agradeço desde ja!!
-
91disakai
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Set 26, 2012 11:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: redes de computadores
- Andamento: cursando
 por young_jedi » Qua Set 26, 2012 12:47
por young_jedi » Qua Set 26, 2012 12:47
1.4
representa a quantidade 108
se fosse 3 na quarta posição seria

ou seja a quantidade seria 648
1.5 bom , nessa ai eu tinha entendido que era 3526 na base 10 e voce queria passar para a base 6 mais pelo jeito, na verdade é
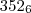
então
fica

sendo que resolvendo isso voce encontra a quantidade representada

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por 91disakai » Qua Set 26, 2012 14:29
por 91disakai » Qua Set 26, 2012 14:29
Valeu man !!!
Tambem estou com dificudade nesse tipo de exercicio
4. Escreva na base 10, os números
4.5. 10B0(13)
4.6. 12CA(16)
1) Converter, para a base decimal, os seguintes números:
h) (1101,01)base 2
2) Converter, os seguintes números, para a base binária:
g) (-3,125) base 10
4) Representar, cada item a seguir, na memória de uma máquina utilizando 16 bits.
g) (-3,125)base 10
VOCE PODERIA ME EXPLICAR PASSO A PASSO como se faz?
-
91disakai
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Set 26, 2012 11:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: redes de computadores
- Andamento: cursando
 por young_jedi » Qua Set 26, 2012 15:07
por young_jedi » Qua Set 26, 2012 15:07
o primeiro esta na base 13
então o simbolos são
0 1 2 3 4 5 6 7 9 A B C
sendo que A vale 10 em decimal,B vale 11, C vale 12
4.5) então calculando
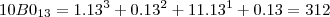
4.6) neste caso temos que ele esta na base 16 ou seja os simbolos sao
0 1 2 3 4 5 6 7 9 A B C D E F
onde em decimal A=10,B=11,C=12,D=13,E=14,F=15
então
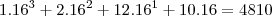
1)

é so calcular
2)
temos que

e

então
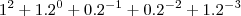
então

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por 91disakai » Qua Set 26, 2012 15:19
por 91disakai » Qua Set 26, 2012 15:19
Valeu mesmo cara !! e desculpa por encomodar !!
-
91disakai
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Set 26, 2012 11:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: redes de computadores
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistemas de numeração] Achar bases diferentes
por armando » Seg Jun 20, 2016 15:06
- 1 Respostas
- 5061 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 09, 2016 14:30
Teoria dos Números
-
- sistema de numeração
por leticiapires52 » Seg Mai 19, 2014 19:59
- 2 Respostas
- 1920 Exibições
- Última mensagem por Russman

Seg Mai 19, 2014 22:07
Teoria dos Números
-
- SISTEMAS DE NUMERAÇÃO
por metalll666 » Qua Jan 12, 2011 00:49
- 0 Respostas
- 1597 Exibições
- Última mensagem por metalll666

Qua Jan 12, 2011 00:49
Progressões
-
- Numeração e Divisibilidade
por vanessaclm » Sáb Fev 25, 2012 14:36
- 1 Respostas
- 1773 Exibições
- Última mensagem por nathyn

Qui Mar 01, 2012 17:42
Álgebra Elementar
-
- Número de divisores e Sistemas de Numeração
por Gustavo R » Sáb Ago 13, 2011 18:05
- 7 Respostas
- 5546 Exibições
- Última mensagem por Molina

Sáb Ago 20, 2011 19:45
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



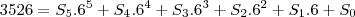
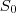
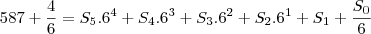

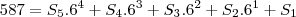


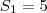



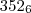 então
então