 por juliahess » Ter Jul 31, 2012 12:55
por juliahess » Ter Jul 31, 2012 12:55
[Operações com números naturais]
Um número tem 15 algarismos e outro 4. O produto deles tem no mínimo ............ algarismos e no máximo ............. algarismos.
Resposta: 18 e 19.
Estou passando problemas do Livro "Questões de Matemática" de Manoel Jairo Bezerra para a minha filha de 10 anos, dentro do conteúdo que ela consegue fazer.
Quando tentamos resolver juntas este problema, chegamos facilmente à 1a parte da resposta. Pois o menor número de 4 algarismos seria 1.000. Então qualquer número de 15 algarismos multiplicado por 1000, teria, no mínimo 18 algarismos. No entanto, não entendemos a parte da quantidade máxima de algarismos (19)? Alguém saberia explicar?
Obrigada desde já,
Julia
-
juliahess
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jul 31, 2012 12:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel Matemática/Informática
- Andamento: formado
 por DanielFerreira » Ter Jul 31, 2012 21:26
por DanielFerreira » Ter Jul 31, 2012 21:26
Olá
Julia,
boa noite e seja bem-vinda!!
Tomemos alguns exemplos p/ facilitar o entendimento!
Multipliquemos os maior número de dois algarismos com o maior de um algarismo:

3 algarismos
Maior de três algarismos com o maior de dois:
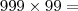
5 algarismos
Note que a quantidade de máxima de algarismos é dada pela SOMA.
Ex 1.:
2 + 1 =
3Ex 2.:
3 + 2 =
5Segue que,
15 + 4 =
19 algarismosEspero ter ajudado!!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [números naturais/inteiros: operações] questão UERJ
por XxXMarlonXxX » Qui Out 04, 2012 16:57
- 10 Respostas
- 9308 Exibições
- Última mensagem por LuizAquino

Sex Out 05, 2012 15:32
Aritmética
-
- [Números naturais] Problema envolvendo dinheiro
por Georges123 » Sáb Fev 16, 2013 00:20
- 2 Respostas
- 1718 Exibições
- Última mensagem por Georges123

Dom Fev 17, 2013 17:09
Teoria dos Números
-
- números naturais
por jose henrique » Dom Ago 15, 2010 15:24
- 2 Respostas
- 1699 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 10:40
Álgebra Elementar
-
- números naturais
por jose henrique » Seg Ago 16, 2010 11:44
- 0 Respostas
- 1174 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 11:44
Álgebra Elementar
-
- números naturais
por jose henrique » Seg Ago 16, 2010 12:31
- 1 Respostas
- 1624 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:06
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 3 algarismos
3 algarismos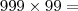 5 algarismos
5 algarismos