''Se n é um número natural, entre n e 2n existe sempre pelo menos um primo.''
Eu consegui demonstrar isso fragmentando a demonstração em 2 partes:
* Se n não é primo (tenho certeza de que está certo)
* Se n é primo (tenho dúvidas a respeito da veracidade dessa parte)
A demonstração é assim:
Dentre os números naturais, podem haver números que satisfazem e que não satisfazem a proposição. Mas sabemos que , dentre os que não satisfazem, existe um que foi o primeiro de todos a não satisfazer. Vamos supor que esse número é n e que ele não seja primo.
Como ele é o primeiro, sabemos que (por hipótese) entre n e 2n não há primos. No entanto isso acarreta em um absurdo, pois o seu antecessor (n - 1) possui entre ele e 2(n - 1), apenas alguns números entre n e 2n e o próprio n que não é primo.
Daí ele passa a ser o primeiro. Esse absurdo prova a primeira parte.
Vamos supor que o primeiro de todos a não satisfazer a proposição seja o n-ésimo primo, ou seja, entre
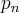e 
não existe um primo. Podemos, com isso, afirmar duas coisas:
(óbvia)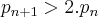
(O próximo primo está fora do intervalo)Subtraíndo a primeira inequação da segunda, vemos o absurdo:
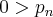
A questão é que eu não tenho certeza quanto á veracidade da segunda proposição. Além disso, pode-se ver claramente que a demonstração depende das duas demonstrações. Está correto ??
