Correção inequação

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Correção inequação

Regras do fórum
Responder

Correção inequação

Mensagempor Andrewo » Qua Jun 06, 2012 13:24

Boa tarde, tô com 2 probleminhas aí que gostaria que vocês corrigissem

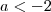1) Se a<-2, os valores de x tais que 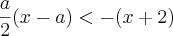\frac{a}{2}(x-a)<-(x+2), são aquelas que satisfazem:

Resp: x>a-2






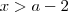
Como eu fiz:
\frac{ax}{2}-\frac{{a}^{2}}{2}<-x-2

ax-{a}^{2}<-2x-4

ax+2x<-4+{a}^{2}

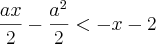
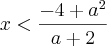x<\frac{-4+{a}^{2}}{a+2} divide por a e 2 em cima e em baixo, fica: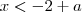

x<-2+a

O resultado ficou parecido mas não bateu o sinal de maior/menor com o gabarito








2) Sejam a e b dois números reais tais que a < b. Se ax-bx>{a}^{2}-{b}^{2}, então:

Resp: x < a + b






Como eu fiz:

x(a-b)>(a-b)(a+b)

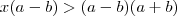
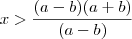x>\frac{(a-b)(a+b)}{(a-b)} simplificando

x> a+b


Novamente a posição do sinal não bateu com a do gabarito :s

Gostaria que me esclarecessem



:y: :y: :y:
Avatar do usuário
Andrewo
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 54
Registrado em: Qui Jan 12, 2012 11:22
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo

Re: Correção inequação

Mensagempor Andrewo » Sex Jun 08, 2012 11:25

Ngm sabe? *-)
Avatar do usuário
Andrewo
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 54
Registrado em: Qui Jan 12, 2012 11:22
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo

Re: Correção inequação

Mensagempor MarceloFantini » Sex Jun 08, 2012 15:50

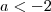A primeira resposta não bateu com o gabarito porque você esqueceu da sua hipótese que a < -2. Lembre-se: quando dizemos que 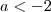a< -2 isto significa que 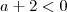a+2 < 0, ou seja, é um número negativo. Ao multiplicar ou dividir uma inequação por um número negativo trocamos a desigualdade, o que você não fez.

Na segunda, novamente você errou ao não perceber isso: se b>a, então b-a> 0 e equivalentemente 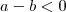a-b<0. Ao dividir ambos lados por a-b você dividiu por um número negativo, portanto trocamos a desigualdade.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo
Responder

Voltar para Álgebra Elementar

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum