 por LuizCarlos » Dom Mai 13, 2012 14:14
por LuizCarlos » Dom Mai 13, 2012 14:14
Olá amigos professores, estou resolvendo uns problemas que envolvem equações do 2 grau com uma incógnita!
Estou aqui vendo a resolução do livro nesse problema, mas não consegui entender como ele encontrou o valor

.
A hipotenusa de um triângulo retângulo tem
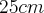
.Determine as medidas dos catetos desse triângulo sabendo que um deles mede

a mais que o outro.
Aplicando o teorema de Pitágoras:
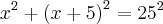
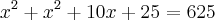
A única coisa que não estou conseguindo entender é de onde ele tirou esse

. Como encontrou esse valor

.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Dom Mai 13, 2012 14:20
por LuizCarlos » Dom Mai 13, 2012 14:20
LuizCarlos escreveu:Olá amigos professores, estou resolvendo uns problemas que envolvem equações do 2 grau com uma incógnita!
Estou aqui vendo a resolução do livro nesse problema, mas não consegui entender como ele encontrou o valor

.
A hipotenusa de um triângulo retângulo tem
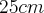
.Determine as medidas dos catetos desse triângulo sabendo que um deles mede

a mais que o outro.
HNI_0002.JPG
Aplicando o teorema de Pitágoras:
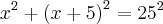
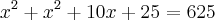
A única coisa que não estou conseguindo entender é de onde ele tirou esse

. Como encontrou esse valor

.
Desconsiderem o tópico, quando criei o tópico, acabei percebendo que

é um produto notável,

, vem do produto notável.

-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problemas do segundo grau II
por Alessandra Cezario » Seg Mai 02, 2011 17:56
- 1 Respostas
- 2606 Exibições
- Última mensagem por TheoFerraz

Seg Mai 02, 2011 18:31
Problemas do Cotidiano
-
- Problemas do Segundo grau III
por Alessandra Cezario » Seg Mai 02, 2011 19:08
- 4 Respostas
- 4157 Exibições
- Última mensagem por TheoFerraz

Seg Mai 02, 2011 20:20
Problemas do Cotidiano
-
- Problemas do Segundo grau médio
por Alessandra Cezario » Ter Mai 03, 2011 17:07
- 2 Respostas
- 4244 Exibições
- Última mensagem por Alessandra Cezario

Qua Mai 04, 2011 16:05
Problemas do Cotidiano
-
- Equação do segundo grau
por VtinxD » Qui Jan 27, 2011 23:03
- 1 Respostas
- 3888 Exibições
- Última mensagem por douglaspezzin

Dom Jun 19, 2011 09:55
Desafios Médios
-
- Equação de segundo grau
por maria cleide » Seg Mai 09, 2011 23:46
- 3 Respostas
- 2686 Exibições
- Última mensagem por FilipeCaceres

Ter Mai 10, 2011 00:43
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.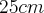 .Determine as medidas dos catetos desse triângulo sabendo que um deles mede
.Determine as medidas dos catetos desse triângulo sabendo que um deles mede  a mais que o outro.
a mais que o outro.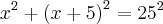
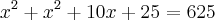
 . Como encontrou esse valor
. Como encontrou esse valor  .
.

 é um produto notável,
é um produto notável, 
