A quantidade de números inteiros compreendidos entre 0 e
4000, que podem ser expressos como a soma de duas ou
mais potências distintas de 5, é igual a:
(A) 54
(B) 55
(C) 56
(D) 57
Gostaria mt de ver a resolução!!Ajuda!! Por favor!!



Pri Ferreira escreveu:A quantidade de números inteiros compreendidos entre 0 e
4000, que podem ser expressos como a soma de duas ou
mais potências distintas de 5, é igual a:
(A) 54
(B) 55
(C) 56
(D) 57
Pri Ferreira escreveu:Gostaria mt de ver a resolução!!
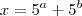

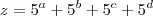

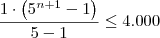
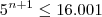
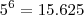 e
e 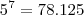 , temos que no máximo n + 1 = 6. Ou seja, no máximo podemos ter 6 parcelas.
, temos que no máximo n + 1 = 6. Ou seja, no máximo podemos ter 6 parcelas.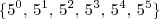 ?
?

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: