paulo nieres escreveu:Eu tenho uma divida de D reais no 1° mês paguei 1/4 do total da divida e 1/5 do que restou no 2° mês, e no 3° mes paguei a terça parte do que restou e finalizei a divida com um pagamento de R$:800,00 qual era o valor de D?
No 1º mês, foi pago
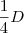
. Sobrou então
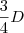
.
No 2º mês, foi pago 1/5 do que restou em relação ao 1º mês. Desse modo, foi pago
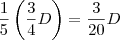
.
Até agora, já foi pago
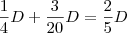
. Sobrou então
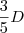
.
No 3º mês, foi pago 1/3 do que restou em relação ao 2º mês. Desse modo, foi pago
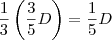
.
Até agora, já foi pago
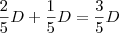
.
Por fim, a dívida foi finalizada com um pagamento de R$ 800,00.
Desse modo, somando
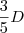
com R$ 800,00 obtemos o valor da dívida.
Temos então que:
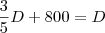
Resolvendo essa equação, obtemos que a dívida é igual a R$ 2.000,00.
paulo nieres escreveu:(...) eu acabei de entrar na faculdade ai essa semana fui fazer uma revisão nos meu conhecimentos de matemática (...)
Para ajudar em sua revisão, eu recomendo que você assista as videoaulas do Nerckie no YouTube:
http://www.youtube.com/nerckie

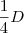 . Sobrou então
. Sobrou então 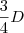 .
.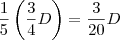 .
.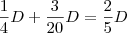 . Sobrou então
. Sobrou então 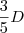 .
.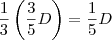 .
.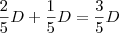 .
.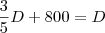

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.