 por sullivan » Ter Jan 24, 2012 13:41
por sullivan » Ter Jan 24, 2012 13:41
Boa tarde Galera queria agradecer pelo ajuda que vocês me deram apoio respondendo algumas dúvidas que tive, fiz a prova do concurso domingo foi facil apenas uma questão que não soube nem começar a resolver rsrs queria que você me desse uma luz pra saber lidar melhor com radiciação.. a pergunta era: Se o produto
![\sqrt[]{18} . \sqrt[3]{16} . x \sqrt[]{18} . \sqrt[3]{16} . x](/latexrender/pictures/7899acfd373e3645f955030e6aa01ff6.png)
é um numero racional, então x pode ser igual a ? por favor galera me ajudem mais uma vez..
-
sullivan
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 23, 2011 10:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Ter Jan 24, 2012 14:03
por LuizAquino » Ter Jan 24, 2012 14:03
sullivan escreveu:Boa tarde Galera queria agradecer pelo ajuda que vocês me deram apoio respondendo algumas dúvidas que tive, fiz a prova do concurso domingo foi facil apenas uma questão que não soube nem começar a resolver rsrs queria que você me desse uma luz pra saber lidar melhor com radiciação.. a pergunta era: Se o produto
![\sqrt{18} \cdot \sqrt[3]{16} \cdot x \sqrt{18} \cdot \sqrt[3]{16} \cdot x](/latexrender/pictures/70b4dc6462bb0a43311c5c2ada1324a0.png)
é um numero racional, então x pode ser igual a ? por favor galera me ajudem mais uma vez
Há infinitos valores que x pode assumir que tornam esse produto racional. Nesse contexto, é necessário analisar as alternativas fornecidas na questão. Por favor, poste também as alternativas.
Por exemplo, se x=0, então esse produto seria igual a 0 (que é racional).
Como outro exemplo, se
![x = \frac{1}{\sqrt{18}\sqrt[3]{16}} x = \frac{1}{\sqrt{18}\sqrt[3]{16}}](/latexrender/pictures/c03bd5754daa6b716f066a1380ea444f.png)
, então esse produto seria igual a 1 (que é racional).
Mais outro exemplo, se
![x = \sqrt{2}\sqrt[3]{4} x = \sqrt{2}\sqrt[3]{4}](/latexrender/pictures/08a76bbac0904636dd55bf6cddb19da9.png)
, então esse produto seria igual a 24 (que é racional).
Note como há várias repostas possíveis!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por sullivan » Ter Jan 24, 2012 14:49
por sullivan » Ter Jan 24, 2012 14:49
Perdão pela a falta de informação rsrs
a)
![\sqrt[6]{16}
b) \sqrt[6]{2}
c) \sqrt[3]{2}
d) \sqrt[]{2} \sqrt[6]{16}
b) \sqrt[6]{2}
c) \sqrt[3]{2}
d) \sqrt[]{2}](/latexrender/pictures/4ab907a528a56f8754ec6e2750a886b7.png)
-
sullivan
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sex Dez 23, 2011 10:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Radiciação dúvida!
por LuizCarlos » Ter Mai 15, 2012 18:57
- 3 Respostas
- 2177 Exibições
- Última mensagem por LuizAquino

Sex Mai 18, 2012 13:26
Álgebra Elementar
-
- Radiciação - Dúvida
por Danilo » Qui Ago 09, 2012 22:37
- 2 Respostas
- 1476 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 00:04
Álgebra Elementar
-
- Dúvida - radiciação
por Danilo » Sex Ago 10, 2012 01:53
- 3 Respostas
- 1701 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 11:22
Álgebra Elementar
-
- Dúvida - {radiciação}
por Danilo » Sex Ago 10, 2012 11:34
- 2 Respostas
- 1615 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 11:47
Álgebra Elementar
-
- Radiciação - dúvida
por Danilo » Sex Ago 10, 2012 18:33
- 2 Respostas
- 1583 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 20:01
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{18} . \sqrt[3]{16} . x \sqrt[]{18} . \sqrt[3]{16} . x](/latexrender/pictures/7899acfd373e3645f955030e6aa01ff6.png) é um numero racional, então x pode ser igual a ? por favor galera me ajudem mais uma vez..
é um numero racional, então x pode ser igual a ? por favor galera me ajudem mais uma vez..

![\sqrt[]{18} . \sqrt[3]{16} . x \sqrt[]{18} . \sqrt[3]{16} . x](/latexrender/pictures/7899acfd373e3645f955030e6aa01ff6.png) é um numero racional, então x pode ser igual a ? por favor galera me ajudem mais uma vez..
é um numero racional, então x pode ser igual a ? por favor galera me ajudem mais uma vez..
é um numero racional, então x pode ser igual a ? por favor galera me ajudem mais uma vez
![x = \frac{1}{\sqrt{18}\sqrt[3]{16}} x = \frac{1}{\sqrt{18}\sqrt[3]{16}}](/latexrender/pictures/c03bd5754daa6b716f066a1380ea444f.png) , então esse produto seria igual a 1 (que é racional).
, então esse produto seria igual a 1 (que é racional).![x = \sqrt{2}\sqrt[3]{4} x = \sqrt{2}\sqrt[3]{4}](/latexrender/pictures/08a76bbac0904636dd55bf6cddb19da9.png) , então esse produto seria igual a 24 (que é racional).
, então esse produto seria igual a 24 (que é racional).
![\sqrt[6]{16}
b) \sqrt[6]{2}
c) \sqrt[3]{2}
d) \sqrt[]{2} \sqrt[6]{16}
b) \sqrt[6]{2}
c) \sqrt[3]{2}
d) \sqrt[]{2}](/latexrender/pictures/4ab907a528a56f8754ec6e2750a886b7.png)

![\sqrt{18} \cdot \sqrt[3]{16}\cdot x = \left(\sqrt{2\cdot 3^2}\right) \cdot \left(\sqrt[3]{2\cdot 2^3}\right) \cdot x \sqrt{18} \cdot \sqrt[3]{16}\cdot x = \left(\sqrt{2\cdot 3^2}\right) \cdot \left(\sqrt[3]{2\cdot 2^3}\right) \cdot x](/latexrender/pictures/dc2d5b8c0aec88cc3f2ac4ea004044e4.png)
![= 6 \cdot \sqrt{2} \cdot \sqrt[3]{2} \cdot x = 6 \cdot \sqrt{2} \cdot \sqrt[3]{2} \cdot x](/latexrender/pictures/de31cb4e2f362185a23d6f1220638ac0.png)
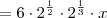
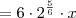
![= 6 \cdot \sqrt[6]{2^5} \cdot x = 6 \cdot \sqrt[6]{2^5} \cdot x](/latexrender/pictures/d4da8336385705a0790bd143abbcd614.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.