1) Se A e B são duas partes quaisque de U, o conjunto
 é denominado diferença simétrica entre A e B.
é denominado diferença simétrica entre A e B.Seja E um conjunto e consideremos sobre o conjunto P(E) das partes de E as operações de Interseção
 e de diferença simétrica
e de diferença simétrica 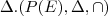 .
.Determinar todos os divisores do zero do anel
 .
.Bom.. todos os divisores do zero são da forma:
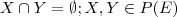
então basta tomarmos:
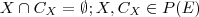 em que
em que 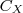 é o complementar de X.
é o complementar de X.Será que está certo isto?
2) Seja A um anel qualquer e
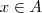 . Se
. Se 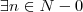 tal que
tal que 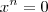 dizemos que o elemento x é nilpotente.
dizemos que o elemento x é nilpotente.a) Dê exemplos de uma infinidade de elementos nilpotentes em um anel não comutativo.
essa eu pensei no anel das matrizes de ordem nxn.
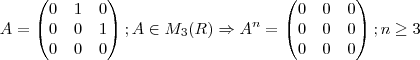
b) Prove que se
 são elementos nilpotentes de A e
são elementos nilpotentes de A e  então
então  é um elemento nilpotente de A.
é um elemento nilpotente de A.Esse não consegui pensar em quase nada. Talvez em elevar a soma a algum n. Por favor dêem-me uma dica.
c) Mostre com um exemplo que a hipótese
 é essencial em (b).
é essencial em (b).esse depende do b então aguardo.
d) Seja x um elemento nilpotente em A. Mostre que, se A possui unidade
 então o elemento
então o elemento  possui inverso multiplicativo (calcule uma fórmula para esse inverso).
possui inverso multiplicativo (calcule uma fórmula para esse inverso).Para possuir um inverso multiplicativo temos:
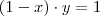 .
.agora temos que achar o y. esse é o problema. Alguém sugere algo?
3) Prove que se A é um anel de divisão então Z(A) é um corpo.
Esse pensei em mostrar que Z(A) é um anel de divisão comutativo, portanto um corpo. está certo isso?
4) Calcule End(Z[i]) e Aut(Q[i]).
sem muitas ideias.
5)Seja A um anel com unidade
 e suponhamos que
e suponhamos que 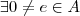 tal que
tal que  (e diz-se um elemento idempotente de A). Se
(e diz-se um elemento idempotente de A). Se  e se
e se 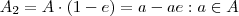 , então prove que:
, então prove que:a)
 e
e  são subaneis de A tais que
são subaneis de A tais que  .
.sem muitas ideias.
b)
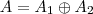 (isto é,
(isto é, 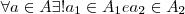 tais que
tais que  ).
).sem muitas ideias.
Agradeço a ajuda de vocês.

