-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Seg Out 31, 2011 23:18
por Molina » Seg Out 31, 2011 23:18
Boa noite.
Coloque o enunciado por inteiro. Apenas com essas informações não é possível.
Fico no aguardo.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizCarlos » Ter Nov 01, 2011 12:21
por LuizCarlos » Ter Nov 01, 2011 12:21
Molina escreveu:Boa noite.
Coloque o enunciado por inteiro. Apenas com essas informações não é possível.
Fico no aguardo.
Beleza, tentei desenhar aqui, mas não ficou perfeito! acho que você vai entender!
A questão fala: Determine x e y:
OP é bissetriz de AÔB.
AÔP
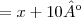
BÔP
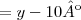
BÔC
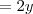
- Anexos
-
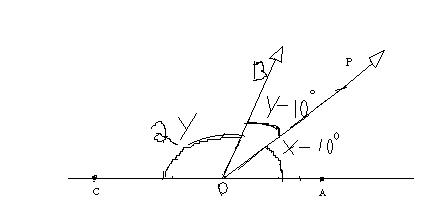
- imagemforum.JPG (8.42 KiB) Exibido 6095 vezes
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Ter Nov 01, 2011 15:12
por MarceloFantini » Ter Nov 01, 2011 15:12
Se OP é bissetriz, podemos afirmar que
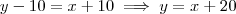
, e daí
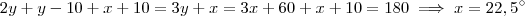
. Para encontrar y basta retornar a outra equação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizCarlos » Ter Nov 01, 2011 16:12
por LuizCarlos » Ter Nov 01, 2011 16:12
MarceloFantini escreveu:Se OP é bissetriz, podemos afirmar que
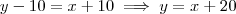
, e daí
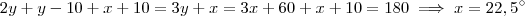
. Para encontrar y basta retornar a outra equação.
Olá MarceloFantini, obrigado por me ajudar! consegui entender, então o centro da atenção nessa questão era a bissetriz, não percebi isso!
Mas essa conta que você fez creio que a parte em que você diz que
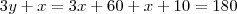
você adicionou 10 no final, então o valor de x está errado, pois esse

não existe, foi cancelado com o
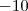
nessa parte aqui :
![2y +y-10+x+10[tex].
Sendo o resultado de [tex]x = 30° 2y +y-10+x+10[tex].
Sendo o resultado de [tex]x = 30°](/latexrender/pictures/0d9ac7278cf71a2bc0642f32b0202024.png)
no livro é exatamente
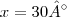
.
No mais está tudo certo, obrigado pela ajuda!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Ter Nov 01, 2011 16:19
por MarceloFantini » Ter Nov 01, 2011 16:19
Realmente, um leve descuido da minha parte, mas a idéia central foi passada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Livia Azevedo » Qui Fev 13, 2014 15:28
por Livia Azevedo » Qui Fev 13, 2014 15:28
Será q vc poderia explicar melhor o q vc fez para chegar a esse resultado Por Favor ? Eh q ñ quero só copiar , quero aprender.
Obrigado !!!!
-
Livia Azevedo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Fev 13, 2014 15:19
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Escola
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão geometria plana relacionada aos ângulos notáveis]
 por Anniemf » Qua Mar 28, 2012 14:33
por Anniemf » Qua Mar 28, 2012 14:33
- 1 Respostas
- 3554 Exibições
- Última mensagem por kelvinJhonson

Sáb Abr 21, 2012 23:20
Geometria Plana
-
- Dúvida - questão - ângulos entre duas retas.
 por Danilo » Sex Jun 22, 2012 21:14
por Danilo » Sex Jun 22, 2012 21:14
- 3 Respostas
- 1682 Exibições
- Última mensagem por Russman

Sáb Jun 23, 2012 19:44
Geometria Analítica
-
- Ângulos
 por admin » Sex Set 07, 2007 06:42
por admin » Sex Set 07, 2007 06:42
- 3 Respostas
- 13555 Exibições
- Última mensagem por Numwantida

Qui Mai 24, 2018 05:06
Pérolas
-
- Angulos ??????
por ByRobert » Qui Set 01, 2011 12:59
- 6 Respostas
- 9037 Exibições
- Última mensagem por LuizAquino

Qui Set 01, 2011 21:24
Trigonometria
-
- ângulos
 por Thays » Sáb Jan 14, 2012 11:59
por Thays » Sáb Jan 14, 2012 11:59
- 6 Respostas
- 4625 Exibições
- Última mensagem por Thays

Qui Jan 19, 2012 09:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
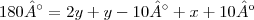

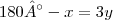
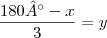


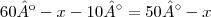

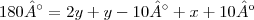

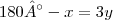
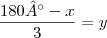


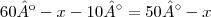


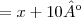
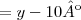
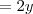

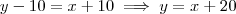 , e daí
, e daí 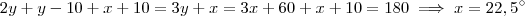 . Para encontrar y basta retornar a outra equação.
. Para encontrar y basta retornar a outra equação.

, e daí
. Para encontrar y basta retornar a outra equação.
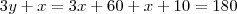 você adicionou 10 no final, então o valor de x está errado, pois esse
você adicionou 10 no final, então o valor de x está errado, pois esse  não existe, foi cancelado com o
não existe, foi cancelado com o 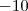 nessa parte aqui :
nessa parte aqui : ![2y +y-10+x+10[tex].
Sendo o resultado de [tex]x = 30° 2y +y-10+x+10[tex].
Sendo o resultado de [tex]x = 30°](/latexrender/pictures/0d9ac7278cf71a2bc0642f32b0202024.png) no livro é exatamente
no livro é exatamente 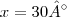 .
.





 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.