 por JoseEduardo » Sex Out 14, 2011 00:53
por JoseEduardo » Sex Out 14, 2011 00:53
Bom dia,
Em questão de potenciação eu sei que:
x elevado a y = x*x*x y vezes
isto é: 2 elevado a 3 = 2*2*2
etc.
Mas queria entender como se faz para elevar x a um número maior que zero e menor que um,
por exemplo:
2 elevado a 0,5
Obrigado!
-
JoseEduardo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Set 10, 2010 01:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
 por TheoFerraz » Sex Out 14, 2011 14:56
por TheoFerraz » Sex Out 14, 2011 14:56
é muito simples.
primeiramente, concorda que

entao podemos escrever
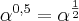
Agora observe a seguinte proposição.
- Sejam a,b e c numeros reais. Entao:
![{a}^{\frac{b}{c}} = \sqrt[c]{{a}^{b}} {a}^{\frac{b}{c}} = \sqrt[c]{{a}^{b}}](/latexrender/pictures/868408b7067f23f3bb99f23c1e509a3e.png)
Facilitou ? =)
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por JoseEduardo » Sex Nov 04, 2011 00:42
por JoseEduardo » Sex Nov 04, 2011 00:42
Nossa, muito. Então 2 elevado a meio é igual a raiz de 2!!
Obrigado mesmo!
-
JoseEduardo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Set 10, 2010 01:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Qual é o menor e o maior valor de x na expressão
por andersontricordiano » Seg Out 03, 2011 16:56
- 1 Respostas
- 3942 Exibições
- Última mensagem por MarceloFantini

Seg Out 03, 2011 21:10
Trigonometria
-
- Potências...
por Estela » Dom Mai 04, 2008 22:15
- 3 Respostas
- 2589 Exibições
- Última mensagem por Glauber2012

Sex Mar 23, 2012 21:23
Álgebra Elementar
-
- Potências
por Jhennyfer » Dom Abr 28, 2013 14:15
- 5 Respostas
- 6765 Exibições
- Última mensagem por Cleyson007

Seg Abr 29, 2013 12:03
Teoria dos Números
-
- Potências
por Jhennyfer » Qui Mai 16, 2013 11:31
- 3 Respostas
- 2215 Exibições
- Última mensagem por Victor Gabriel

Qui Mai 16, 2013 13:12
Álgebra Elementar
-
- Maior valor
por thadeu » Qua Nov 25, 2009 16:17
- 4 Respostas
- 2945 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 22:14
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 entao podemos escrever
entao podemos escrever 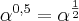
![{a}^{\frac{b}{c}} = \sqrt[c]{{a}^{b}} {a}^{\frac{b}{c}} = \sqrt[c]{{a}^{b}}](/latexrender/pictures/868408b7067f23f3bb99f23c1e509a3e.png)



 .
.
 :
: