 por ginrj » Ter Mar 10, 2009 20:24
por ginrj » Ter Mar 10, 2009 20:24
Olá amigos, trabalhando umas questoes do meu livro tive duvida em 3 questoes ^^ bobas + nao consigo resolvelas aehhuaehuae, gostaria de uma ajuda da galera ai pra que eu possa começar a calcular elas (por favor nao de resposta =D )


![\sqrt[4]{72} : \sqrt[2]{6} \sqrt[4]{72} : \sqrt[2]{6}](/latexrender/pictures/edbe97dc9a40aa696ce562fcc46ec432.png)
são essas acima, na segunda questão eu consegui ir ate um certo ponto + dava algo errado, nao consigo saber o que é ^^
Os números governam o Universo
-
ginrj
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Sex Mar 06, 2009 18:28
- Localização: Rio de Janeiro
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Pré.Militar
- Andamento: cursando
 por Marcampucio » Ter Mar 10, 2009 21:54
por Marcampucio » Ter Mar 10, 2009 21:54
consulte um livro com as regras de potenciação. Ficam umas dicas:
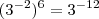
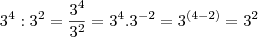
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por Molina » Qua Mar 11, 2009 12:53
por Molina » Qua Mar 11, 2009 12:53
Bom dia.
Acho que com as dicas do Marcampucio você ja consegue resolver sem problemas suas dúvidas sobre potenciação.
Sobre a dúvida na raíz lembre-se que você precisa igualar os índices.
Desta forma:
![\sqrt[2]{{6}^{1}}=\sqrt[4]{{6}^{2}}=\sqrt[4]{36} \sqrt[2]{{6}^{1}}=\sqrt[4]{{6}^{2}}=\sqrt[4]{36}](/latexrender/pictures/b3a8c5ae18e8712470fdb4a49af136c1.png)
Note que eu multipliquei por 2 o índice e o expoente que estava no radicando, para conseguir que o índice ficasse igual a outra raiz.
Abraços e bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por ginrj » Qua Mar 11, 2009 16:57
por ginrj » Qua Mar 11, 2009 16:57
mtoo obrigado, agora consegui resolver os exercicios

Os números governam o Universo
-
ginrj
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Sex Mar 06, 2009 18:28
- Localização: Rio de Janeiro
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Pré.Militar
- Andamento: cursando
 por ginrj » Qua Mar 11, 2009 19:32
por ginrj » Qua Mar 11, 2009 19:32
so confirmando, o primeiro deu 3^-6 , o segundo deu -12 e o terceiro deu 6 raiz quarta de 2
Os números governam o Universo
-
ginrj
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Sex Mar 06, 2009 18:28
- Localização: Rio de Janeiro
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Pré.Militar
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potência e Raízes
por gigante2010 » Qua Out 20, 2010 22:51
- 10 Respostas
- 7844 Exibições
- Última mensagem por Luanita

Dom Mai 15, 2011 13:23
Tópicos sem Interação (leia as regras)
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3685 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3768 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8596 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8111 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\sqrt[4]{72} : \sqrt[2]{6} \sqrt[4]{72} : \sqrt[2]{6}](/latexrender/pictures/edbe97dc9a40aa696ce562fcc46ec432.png)



![\sqrt[4]{72} : \sqrt[2]{6} \sqrt[4]{72} : \sqrt[2]{6}](/latexrender/pictures/edbe97dc9a40aa696ce562fcc46ec432.png)

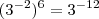
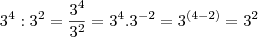

![\sqrt[2]{{6}^{1}}=\sqrt[4]{{6}^{2}}=\sqrt[4]{36} \sqrt[2]{{6}^{1}}=\sqrt[4]{{6}^{2}}=\sqrt[4]{36}](/latexrender/pictures/b3a8c5ae18e8712470fdb4a49af136c1.png)




