 por m0x0 » Seg Set 12, 2011 17:10
por m0x0 » Seg Set 12, 2011 17:10
Boas a todos,
Estou perante uma dúvida de como provar o seguinte por indução:
Mostrar que
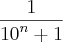
tem expansão puramente periódica com período 2n.
Como

nunca é divisível nem por 2 nem por 5, temos

então estamos perante uma dízima puramente periódica.
Para demonstrar que o período é k=2n, penso que por indução se possa calcular:
Caso base:
Temos que P(1):
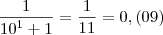
, ou seja, período 2.
Temos que P(2):

, ou seja, período 4.
Temos que P(3):
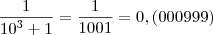
, ou seja, período 6.
etc...
Passo de Indução:

Temos que:
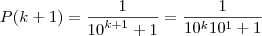
A minha dúvida é passar daqui e provar que tem período sempre k=2n (pelos exemplos vemos que sim, mas falta a prova).
Se alguém me puder ajudar agradecia.
Abraço!
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Encontre a fração geratriz da seguintes dizimas periódicas
por andersontricordiano » Sáb Abr 16, 2011 15:46
- 1 Respostas
- 2832 Exibições
- Última mensagem por Abelardo

Sáb Abr 16, 2011 16:23
Progressões
-
- funções periódicas (exercício do ime de 1995)
por carlospires78 » Ter Out 27, 2009 09:19
- 1 Respostas
- 4907 Exibições
- Última mensagem por BlackFoxes

Sáb Dez 26, 2009 05:08
Funções
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2680 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- indução
por gramata » Qua Set 02, 2009 16:55
- 0 Respostas
- 1233 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:55
Seminário de Resolução de Problemas
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 3063 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
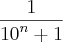 tem expansão puramente periódica com período 2n.
tem expansão puramente periódica com período 2n. nunca é divisível nem por 2 nem por 5, temos
nunca é divisível nem por 2 nem por 5, temos  então estamos perante uma dízima puramente periódica.
então estamos perante uma dízima puramente periódica.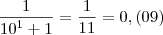 , ou seja, período 2.
, ou seja, período 2. , ou seja, período 4.
, ou seja, período 4.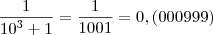 , ou seja, período 6.
, ou seja, período 6.
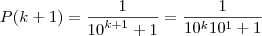


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.