 por wanessa » Dom Ago 21, 2011 21:12
por wanessa » Dom Ago 21, 2011 21:12
Um comerciante compra calças, camisas e saias e as revende com lucro de 20%, 40% e 30%,
respectivamente. O preço x que o comerciante paga por uma calça é três vezes o que ele paga por uma
camisa e duas vezes o que ele paga por uma saia.
Um certo dia, um cliente comprou duas calças, duas camisas e duas saias e obteve um desconto de 10%
sobre o preço total.
b) Qual o lucro aproximado, em porcentagem, obtido pelo comerciante nessa venda?
SEI QUE O CLIENTE PAGOU PELA COMPRA = 4,17x
O preço de custo dos produtos vendidos foi:
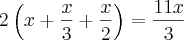
Lucro = Venda - Custo
4,17x -
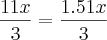
, correspondendo a

%
PQ É DIVIDIDO O LUCRO PELO CUSTO???? NÃO DEVERIA SER FEITO REGRA DE 3????
-
wanessa
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mai 07, 2011 15:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Ago 22, 2011 17:39
por LuizAquino » Seg Ago 22, 2011 17:39
wanessa escreveu:PQ É DIVIDIDO O LUCRO PELO CUSTO???? NÃO DEVERIA SER FEITO REGRA DE 3????
Qual o problema? Aplicando a regra de três você acabaria fazendo essa divisão de qualquer maneira!
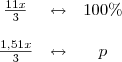
De onde obtemos:

Além disso, vale lembrar que para descobrir a porcentagem que o número
a representa do número
b, basta fazer a operação
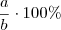
. Por exemplo, a porcentagem que 2 representa de 5 é
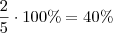
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fuvest - equaçao!
por Artur » Qua Mar 10, 2010 16:33
- 4 Respostas
- 3900 Exibições
- Última mensagem por Artur

Qua Mar 10, 2010 19:00
Sistemas de Equações
-
- equação fuvest 84
por carlos84 » Qui Fev 09, 2012 12:57
- 2 Respostas
- 3178 Exibições
- Última mensagem por carlos84

Qui Fev 09, 2012 17:15
Funções
-
- Equação trigonométrica (FUVEST)
por Ananda » Ter Mar 04, 2008 10:09
- 3 Respostas
- 5289 Exibições
- Última mensagem por admin

Ter Mar 04, 2008 13:46
Trigonometria
-
- (FUVEST) A equação matricial...
por manuoliveira » Seg Set 06, 2010 01:34
- 3 Respostas
- 10506 Exibições
- Última mensagem por rafael_ferramenteiro

Dom Mai 18, 2014 15:05
Matrizes e Determinantes
-
- (FUVEST)equação do 2 grau
por natanskt » Sex Out 22, 2010 11:46
- 1 Respostas
- 10825 Exibições
- Última mensagem por DanielFerreira

Qui Out 28, 2010 16:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
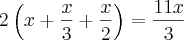
 , correspondendo a
, correspondendo a %
%

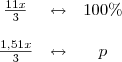

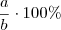 . Por exemplo, a porcentagem que 2 representa de 5 é
. Por exemplo, a porcentagem que 2 representa de 5 é 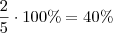 .
.