![\left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}} \left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}}](/latexrender/pictures/3ab38a568fa51bce6f8b2a28e8a1c5d7.png) , ok?
, ok?minha duvida é a seguinte , no caso
![\left(\sqrt[]{a+1} \right){}^{2} \left(\sqrt[]{a+1} \right){}^{2}](/latexrender/pictures/a7f63cd3a1570650d28eb6e5e53e81cf.png) , eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?
, eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?
![\left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}} \left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}}](/latexrender/pictures/3ab38a568fa51bce6f8b2a28e8a1c5d7.png) , ok?
, ok?![\left(\sqrt[]{a+1} \right){}^{2} \left(\sqrt[]{a+1} \right){}^{2}](/latexrender/pictures/a7f63cd3a1570650d28eb6e5e53e81cf.png) , eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?
, eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?


LuizAquino escreveu:
![\sqrt[n]{a^m}= a^\frac{m}{n} \sqrt[n]{a^m}= a^\frac{m}{n}](/latexrender/pictures/86d4ba6090aaf3eaca6cf235f488ae05.png)


Claudin escreveu:
Por isso logicamente, quando elevamos uma raiz ao quadrado, pode retirar a raiz.
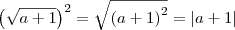

Tome cuidado!
Perceba que não se pode simplesmente "retirar a raiz" e ficar apenas com o radicando.
O que sobra após a simplificação é o módulo do radicando.
![\sqrt[n]{a^m}= a^\frac{m}{n} \sqrt[n]{a^m}= a^\frac{m}{n}](/latexrender/pictures/86d4ba6090aaf3eaca6cf235f488ae05.png)

![\sqrt[]{5x+3}+\sqrt[]{7x-5}=\sqrt[]{4-2x} \sqrt[]{5x+3}+\sqrt[]{7x-5}=\sqrt[]{4-2x}](/latexrender/pictures/d17962d7dca9ce4bb36aefc77f7b8dc2.png)

![\sqrt[2]{x^1}= \sqrt[2]{16^1}\Rightarrow (x^\frac{1}{2})^2= (16^\frac{1}{2})^2\Rightarrow x^\frac{2}{2}=16^\frac{2}{2}\Rightarrow x=16 \sqrt[2]{x^1}= \sqrt[2]{16^1}\Rightarrow (x^\frac{1}{2})^2= (16^\frac{1}{2})^2\Rightarrow x^\frac{2}{2}=16^\frac{2}{2}\Rightarrow x=16](/latexrender/pictures/f995176041ecae5d1ad8ef85cb21e535.png)


Claudin escreveu:Mesmo utilizando a propriedade -->
ficaria em módulo? Só ficaria se eu resolvesse extraindo a raiz quadrada não?
![\sqrt[n]{x^n} = \begin{cases}|x|,\,\textrm{se } n \textrm{ par;} \\ x,\,\textrm{se } n \textrm{ \'impar;}\end{cases} \sqrt[n]{x^n} = \begin{cases}|x|,\,\textrm{se } n \textrm{ par;} \\ x,\,\textrm{se } n \textrm{ \'impar;}\end{cases}](/latexrender/pictures/a018a371f7320e783c2bebe058a6bc88.png)


theSinister escreveu:ah entendi, mas então quando o índice das raízes for 3 por um exemplo, eu elevo os dois lados ao cubo, e assim sucessivamente? essa é a regra?
theSinister escreveu:e quando na mesma equação tiver raízes de índices diferentes, o que fazer?


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes