nota. Faltam apenas 4 e, 16 já resovidos. Não temos mais idéia do que fazer. Peço por favor
sua ajuda.
1) Sendo n um número natural, a expressão
 é igual a:
é igual a:Neste exercício tentamos resolver como função exponecial e, também aplicando a distributiva.
2) Se n pertence a N e n>1, então o valor de
![\sqrt[n]{20/{4}^{n+2}+{2}^{2n+2}} \sqrt[n]{20/{4}^{n+2}+{2}^{2n+2}}](/latexrender/pictures/06e08c4cdc0300d6f04b6ad1590f189f.png)
Aqui tentamos resolver o denominador por exponencial e, simplicar o que era possível.
3) O valor de
 , para x=111 e
, para x=111 e y=112, é:
No exercício em questão tentamos aplicar as regras de fatoração, evidência e simplificação.
4) Calcule o valor de
 , sabendo que
, sabendo que 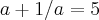 .
.No último exercício tentamos calcular o mmc e, depois montamos uma equação do 2º grau,
mas como nos casos anteriores não conseguimos finalizar.
Agradecemos por sua atenção,
Um abraço.


 ,
, 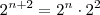 ,
,  ,
,  ,
, 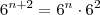 e que podemos fazer
e que podemos fazer 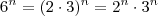 . Tente fazer o primeiro usando isso.
. Tente fazer o primeiro usando isso. .
.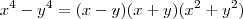 e
e  .
. e veja o que acontece.
e veja o que acontece.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.