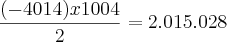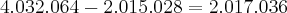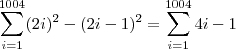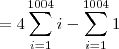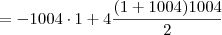Que curioso, hoje mesmo estava procurando algum material básico sobre somatório e produtório, que dizem ser ótimas ferramentas matemáticas... na parte ''PEDIDOS DE MATERIAIS'' desse fórum, deixei um tópico a procura desse material.
Bom professor, como não sei usar somatório, tentei resolver a questão de outra forma. Veja como fiz, por favor. O senhor pode conferir se está correta a resposta?
Coloquei que 2008 é igual a x, logo terei
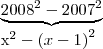

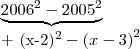
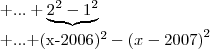
Percebi que existem 1004 ''parcelas'' no total. Quando começei a resolver cada parcela vi que cada uma é o resultado de uma subtração em que

é o minuendo e que o subtraendo é um número natural, onde todos os subtraendos formam uma P.A. de razão

.
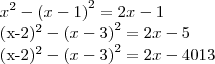
Fiquei com a seguinte expressão -->
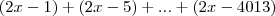
Logo terei

e usei a fórmula da soma de uma P.A. para encontrar o valor da soma de todos os subtraendos
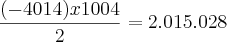
Como resposta encontrei
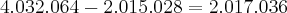
Estou certo? Acho que com somatório deve ser mil vezes mais simples, mas não sei utilizar a ferramenta. Caso o senhor tenha alguma apostila falando sobre somatório ou produtório e puder disponibilizar, ficarei gratíssimo.
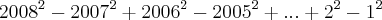 ?
?

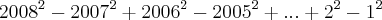 ?
?
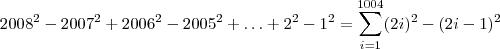 .
.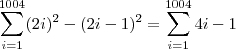 .
.
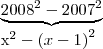

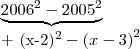
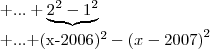
 é o minuendo e que o subtraendo é um número natural, onde todos os subtraendos formam uma P.A. de razão
é o minuendo e que o subtraendo é um número natural, onde todos os subtraendos formam uma P.A. de razão  .
.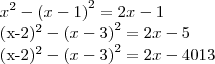
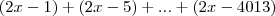
 e usei a fórmula da soma de uma P.A. para encontrar o valor da soma de todos os subtraendos
e usei a fórmula da soma de uma P.A. para encontrar o valor da soma de todos os subtraendos