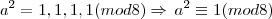-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478555 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533713 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 497249 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 711184 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2131115 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Caeros » Sáb Mar 19, 2011 18:34
por Caeros » Sáb Mar 19, 2011 18:34
Estou estudando o material que postei neste fórum e tenho algumas dúvidas:
Mostre que

não tem soluções:
Solução:
Para qualquer que seja x inteiro, temos:
x

0,1,2,3,4,5,6,7(mod8)

aqui entendo que é aplicada a propriedade que diz: "Sabemos que a

b(modm)

a = b+mk, para algum k

Z. Neste
caso b coincidirá com o resto da divisão euclidiana de "a " por "m ",se e somente,
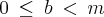
"
logo,
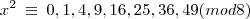

aqui compreendo que foi aplicada a
propriedade que diz: "

Daí,
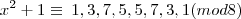

já aqui não consigo compreender qual propriedade foi aplicada ou como chegou a estes valores????






continuando:
Ou melhor


como não entendi anteriormente não entendi como estes valores provam a insolubilidade!!!




O que garante a insolubilidade de

-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Renato_RJ » Sáb Mar 19, 2011 20:56
por Renato_RJ » Sáb Mar 19, 2011 20:56
Eu não consegui chegar neste resultado, veja o que eu fiz:
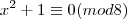
Mas montando as classes de equivalência módulo 8 ou sistema completo de resto módulo 8 para x teremos:
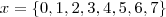
Fazendo

e usando a propriedade já citada, teremos:

Como estamos trabalhando com as classes de resto, teremos:

Logo teremos:

Então teremos:
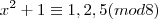
Aqui você percebe que não há solução para
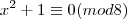
, pois o resto da divisão será 1, 2 ou 5...
Não sei se estou certo, mas pela lógica, parece que sim... Se estou errando em algum lugar, gostaria de saber a onde (fiquei curioso)...
Editado pela última vez por
Renato_RJ em Sáb Mar 19, 2011 22:59, em um total de 1 vez.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Renato_RJ » Sáb Mar 19, 2011 22:57
por Renato_RJ » Sáb Mar 19, 2011 22:57
Esse seu caso me lembrou a seguinte demonstração:
Provar que, qualquer que seja o inteiro ímpar a, o resto da divisão de

por 8 é 1.
Solução:
Os restos possíveis da divisão de a por 8 são 1, 3, 5 ou 7 (chamamos isso de sistema reduzido de resíduo módulo 8, pois só estão nele os restos relativamente primos a 8).
Logo:
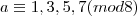
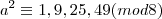
Como
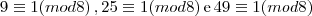
teremos:
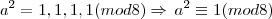
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Caeros » Dom Mar 20, 2011 00:38
por Caeros » Dom Mar 20, 2011 00:38
Olá Renato, obrigado por colaborar,mas quem quer saber tem que perguntar:
estou começando a estudar este assunto, então vou lhe perguntar:
1) O que vc está dizendo com "classes de equivalência módulo 8"? sei que congruência é uma relação de equivalência, então vc está dizendo que x = {0, 1, 2, 3, 4, 5, 6, 7} é o conjunto dos restos que se podem ter na divisão por 8 ou os valores que x pode assumir? Quer dizer estes números se relacionam com 8 por ser os retos relacionados a ele na divisão?
2) e o sistema completo de resto módulo 8 para x, então este é o conjunto de números que podem ser restos?
3) de onde saiu
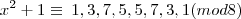
? na resposta que postei pois tirei do material e se estiver errado tenho que corrigir a fonte ou seja onde consegui o material.
Mais uma vez obrigado está me ajudando bastante.

-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Renato_RJ » Dom Mar 20, 2011 03:27
por Renato_RJ » Dom Mar 20, 2011 03:27
Caeros escreveu:Olá Renato, obrigado por colaborar,mas quem quer saber tem que perguntar:
estou começando a estudar este assunto, então vou lhe perguntar:
1) O que vc está dizendo com "classes de equivalência módulo 8"? sei que congruência é uma relação de equivalência, então vc está dizendo que x = {0, 1, 2, 3, 4, 5, 6, 7} é o conjunto dos restos que se podem ter na divisão por 8 ou os valores que x pode assumir? Quer dizer estes números se relacionam com 8 por ser os retos relacionados a ele na divisão?
Caeros, concordo plenamente, se deseja saber tem mais é que perguntar !!!
Lembre-se que estamos tratando de divisão pelo algoritmo de Euclides, isto é, x = 8k + r, onde r é o resto.. As classes de equivalência na verdade são o que chamamos de partições, elas representam os restos das divisões por 8 (neste caso) então cada classe dessa é um conjunto separado, veja:
Quando falamos de classe 0, por exemplo, estamos falando de todos os números inteiros cuja a divisão por 8 dá resto zero, então 0 = {...,8,16,32,48,..} e quando falamos de classe 1 estamos falando do conjunto dos números inteiros cuja a divisão por 8 dá resto 1, então 1 = {...,9,17,33,49,..}.
Caeros escreveu:2) e o sistema completo de resto módulo 8 para x, então este é o conjunto de números que podem ser restos?
Exatamente, como eu disse anteriormente... Classe 3 significa todos os inteiros cuja a divisão por 8 tenha resto 3, então 3 = {...,11,19,35,51,..}.
Caeros escreveu:3) de onde saiu
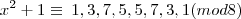
? na resposta que postei pois tirei do material e se estiver errado tenho que corrigir a fonte ou seja onde consegui o material.
Mais uma vez obrigado está me ajudando bastante.

Boa pergunta, eu também quero saber... Se me apresentassem esse problema sem a demonstração, eu teria feito do jeito que escrevi, eu também não entendi a onde o autor obteve esses números e sabe o que é mais interessante ?? Andei pesquisando na internet agora e vi um pdf onde o autor faz o mesmo exercício da mesma maneira, agora eu fiquei confuso, pois devo ter errado em algum lugar (ou no raciocínio da questão)... Vamos esperar o pessoal mais experiente (Luiz Aquino, Molina ou o Fantini) lerem a questão e postarem suas opiniões ou correções.
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matéria de Divisibilidade e Congruências
por EREGON » Ter Mai 12, 2015 11:49
- 1 Respostas
- 2075 Exibições
- Última mensagem por adauto martins

Qua Mai 13, 2015 13:24
Teoria dos Números
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 6970 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 2764 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2297 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2311 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 17 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 não tem soluções:
não tem soluções: 0,1,2,3,4,5,6,7(mod8)
0,1,2,3,4,5,6,7(mod8) aqui entendo que é aplicada a propriedade que diz: "Sabemos que a
aqui entendo que é aplicada a propriedade que diz: "Sabemos que a  b(modm)
b(modm)  a = b+mk, para algum k
a = b+mk, para algum k  Z. Neste
Z. Neste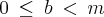 "
"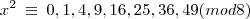
 aqui compreendo que foi aplicada a
aqui compreendo que foi aplicada a 
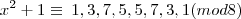
 já aqui não consigo compreender qual propriedade foi aplicada ou como chegou a estes valores????
já aqui não consigo compreender qual propriedade foi aplicada ou como chegou a estes valores???? 



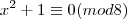
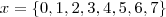
 e usando a propriedade já citada, teremos:
e usando a propriedade já citada, teremos:


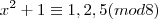

 por 8 é 1.
por 8 é 1.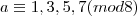
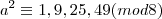
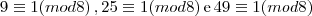 teremos:
teremos: