Sejam E= {-3,-2,-1,0, 1,2,3} e R= {(x,y)
 E x E/x +
E x E/x +  =y +
=y + 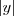 }. Mostre que R é uma relação de equivalência e descreva E/R.
}. Mostre que R é uma relação de equivalência e descreva E/R.Solução:
R é reflexiva pois (1,1),(2,2),(3,3),(-1,-1),(-2,-2),(-3,-3),(0,0)
 R;
R;R é simétrica pois (1,1),(2,2),(3,3),(-1,-1),(-2,-2),(-3,-3),(0,0)
 R;
R;R é transitiva pois (1,1),(2,2),(3,3),(-1,-1),(-2,-2),(-3,-3),(0,0)
 R;
R;E/R:
[1]= {
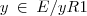 }={1};
}={1};[2]= {
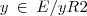 }={2};
}={2};[3]= {
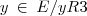 }={3};
}={3};[0]= {
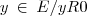 }={0};
}={0};[-1]= {
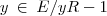 }={-1};
}={-1};[-2]= {
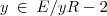 }={-2};
}={-2};[-3]= {
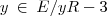 }={-3};
}={-3};então E/R penso ser: E/R={{0},{1},{2},{3},{-1},{-2},{-3}};
mas no gabarito tem E/R={{-3,-2,-1,0},{1},{2},{3}}, porquê?


![[a] = \{s \,|\, (s,\, a) \in R\} [a] = \{s \,|\, (s,\, a) \in R\}](/latexrender/pictures/c727308a5467e1769f8565f91dae7169.png)
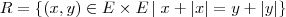 .
.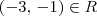 , já que
, já que ![-3\not\in [-1] -3\not\in [-1]](/latexrender/pictures/97110ce61fded09052a254dc4dfeae05.png) .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.