 por Caeros » Ter Mar 08, 2011 13:13
por Caeros » Ter Mar 08, 2011 13:13
Prezados colegas ajude-me a compreender a seguinte sentença e solução:
Seja a sequência  = 1,
= 1,  = 3 e
= 3 e  =
= 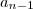 +
+  ,
, com n
com n  3. Mostre que
3. Mostre que
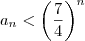 ,
, n
n 
Solução. Seja P (n) : a proposição: a <  ,
, n
n  .
.
A afirmação P (1) é verdadeira porque
 = 1 <
= 1 < 
Seja k  ; arbitrário e suponha-se que P (k) é verdadeira, isto é
; arbitrário e suponha-se que P (k) é verdadeira, isto é
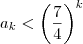 ,(hipótese de indução)
,(hipótese de indução)
pretende provar-se que P (k +1) é verdadeira, ou seja,

Usando a hipótese de indução obtém-se:
 já a partir daqui não compreendo esta igualdade????????????
já a partir daqui não compreendo esta igualdade????????????  .
. 

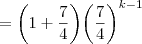
Uma vez que:

Conclui-se que:
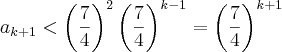
O princÌpio de indução finita permite assim concluir que a afirmação P (n)
é veradeira, para todo o n  .
.
Editado pela última vez por
Caeros em Ter Mar 08, 2011 16:43, em um total de 1 vez.
-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Mar 08, 2011 16:42
por MarceloFantini » Ter Mar 08, 2011 16:42
Abelardo, ele não quer provar nenhuma dessas coisas.
A relação que você sabe é que pra encontrar um elemento, você soma os dois anteriores. Usando isso:
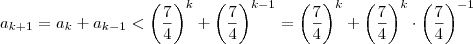
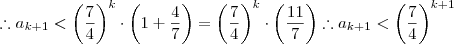
Demonstrado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caeros » Ter Mar 08, 2011 17:38
por Caeros » Ter Mar 08, 2011 17:38
Olá Fantini obrigado deu uma clareada e percebi que a própria resolução está apresentando alguns erros!! esta resolução retirei de um livro, e não estava compreendendo, mas a dúvida já é outra!
Não compreendi como você partindo da expressão:
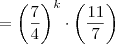
chegou a expressão:

na resposta que vc postou??

aguardo

-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caeros » Ter Mar 08, 2011 21:40
por Caeros » Ter Mar 08, 2011 21:40
Valeu Fantini por colaborar!

-
Caeros
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Seg Mai 25, 2009 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Mar 08, 2011 21:44
por MarceloFantini » Ter Mar 08, 2011 21:44
Sem problemas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra] Princípio da indução finita com desigualdades
por Victor Franca » Seg Mar 04, 2013 21:05
- 1 Respostas
- 2709 Exibições
- Última mensagem por young_jedi

Seg Mar 04, 2013 23:43
Álgebra Elementar
-
- Indução finita !
 por Lucas Alves Ribeiro » Dom Mar 10, 2013 22:47
por Lucas Alves Ribeiro » Dom Mar 10, 2013 22:47
- 0 Respostas
- 1214 Exibições
- Última mensagem por Lucas Alves Ribeiro

Dom Mar 10, 2013 22:47
Álgebra Elementar
-
- Princípio da Indução Finita
por Fontelles » Dom Jan 17, 2010 14:42
- 9 Respostas
- 105677 Exibições
- Última mensagem por Vennom

Qui Abr 26, 2012 23:04
Funções
-
- PIF - Principio da Indução Finita
por ederj » Seg Jun 28, 2010 13:35
- 3 Respostas
- 8047 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 20:01
Funções
-
- Indução Finita FIbonacci
por Garota nerd » Ter Mai 03, 2011 17:52
- 3 Respostas
- 2958 Exibições
- Última mensagem por Garota nerd

Qui Mai 05, 2011 00:43
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 = 1,
= 1,  = 3 e
= 3 e  =
= 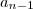 +
+  ,
, com n
com n  3. Mostre que
3. Mostre que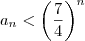 ,
, n
n 
 ,
, n
n  .
. = 1 <
= 1 < 
 ; arbitrário e suponha-se que P (k) é verdadeira, isto é
; arbitrário e suponha-se que P (k) é verdadeira, isto é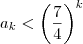 ,(hipótese de indução)
,(hipótese de indução)
 já a partir daqui não compreendo esta igualdade????????????
já a partir daqui não compreendo esta igualdade???????????? 

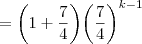

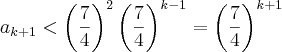
 .
.

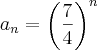 ou
ou 

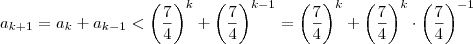
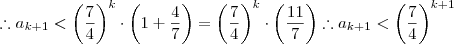


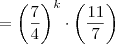 chegou a expressão:
chegou a expressão:  na resposta que vc postou??
na resposta que vc postou?? 
 , então:
, então: 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
