 por vanessitah » Seg Mar 07, 2011 14:04
por vanessitah » Seg Mar 07, 2011 14:04
Na seguinte expressao:
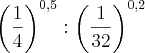
.
Sei que na divisao de numero fracionario, multiplico a primeira fraçao, pelo inverso da segunda.
Segui o seguinte raciocinio:
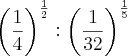
=

=
Esta certo? Como soluciono o expoente fracionario da fraçao!
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por vanessitah » Seg Mar 07, 2011 14:53
por vanessitah » Seg Mar 07, 2011 14:53
vanessitah escreveu:Na seguinte expressao:
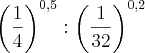
.
Sei que na divisao de numero fracionario, multiplico a primeira fraçao, pelo inverso da segunda.
Segui o seguinte raciocinio:
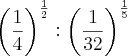
=

=
Esta certo? Como soluciono o expoente fracionario da fraçao!
Primeiro faço o inverso da potencia e depois multiplico a segunda fraçao invertida?
![{\left(\frac{1}{4} \right)}^{\frac{1}{2}}:\left(\frac{1}{32} \right)}^{\frac{1}{5}} =\sqrt[2]{\frac{1}{4}} : \sqrt[5]{\frac{1}{32}}= \sqrt[2]{\frac{1}{4}}.\sqrt[5]{\frac{32}{1}}= {\left(\frac{1}{4} \right)}^{\frac{1}{2}}:\left(\frac{1}{32} \right)}^{\frac{1}{5}} =\sqrt[2]{\frac{1}{4}} : \sqrt[5]{\frac{1}{32}}= \sqrt[2]{\frac{1}{4}}.\sqrt[5]{\frac{32}{1}}=](/latexrender/pictures/b0c9d7fbee0f91d27f6c84e4f84dc4dc.png)
???
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Frações] Regra de frações
por raymondtfr » Dom Nov 02, 2014 16:49
- 4 Respostas
- 3318 Exibições
- Última mensagem por Russman

Dom Nov 02, 2014 23:57
Aritmética
-
- FRAÇÕES
por csantos » Sex Ago 29, 2008 16:33
- 1 Respostas
- 3262 Exibições
- Última mensagem por admin

Sex Ago 29, 2008 16:47
Álgebra Elementar
-
- frações
por suryah » Qua Out 20, 2010 18:28
- 3 Respostas
- 3570 Exibições
- Última mensagem por DanielFerreira

Seg Nov 29, 2010 19:54
Álgebra Elementar
-
- Frações
por Sergio Batista Lima » Qua Ago 31, 2011 21:53
- 1 Respostas
- 1913 Exibições
- Última mensagem por Neperiano

Sex Set 02, 2011 16:14
Álgebra Elementar
-
- frações
por Manuella Vieira » Ter Mar 20, 2012 19:45
- 2 Respostas
- 1648 Exibições
- Última mensagem por MarceloFantini

Ter Mar 20, 2012 20:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
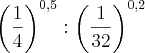 .
. 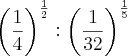 =
=  =
=
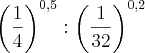 .
. 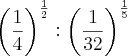 =
=  =
=
.
=
=
![{\left(\frac{1}{4} \right)}^{\frac{1}{2}}:\left(\frac{1}{32} \right)}^{\frac{1}{5}} =\sqrt[2]{\frac{1}{4}} : \sqrt[5]{\frac{1}{32}}= \sqrt[2]{\frac{1}{4}}.\sqrt[5]{\frac{32}{1}}= {\left(\frac{1}{4} \right)}^{\frac{1}{2}}:\left(\frac{1}{32} \right)}^{\frac{1}{5}} =\sqrt[2]{\frac{1}{4}} : \sqrt[5]{\frac{1}{32}}= \sqrt[2]{\frac{1}{4}}.\sqrt[5]{\frac{32}{1}}=](/latexrender/pictures/b0c9d7fbee0f91d27f6c84e4f84dc4dc.png) ???
???
