 por MateusJunior » Qui Mar 03, 2011 18:41
por MateusJunior » Qui Mar 03, 2011 18:41
Boa noite, este é meu primeiro tópico, preciso de ajuda em um cáuculo de física urgente, trata-se de uma equação onde devo achar a incógnita Q, preciso do processo para chegar ao resultado para que eu possa compreender melhor
Minha dificuldade fica em eliminar o 0,1, e em algumas propriedades
Cáuculo:
![\[0,1 = 9\cdot 10^{9}\cdot \frac{Q\cdot Q}{2^{2}}\] \[0,1 = 9\cdot 10^{9}\cdot \frac{Q\cdot Q}{2^{2}}\]](/latexrender/pictures/67dcf2a856a6216affe88d93c03dedbe.png)
Uma parte do cáuculo antes de chegar à resposta:
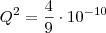
Resposta:

Preciso de ajuda o mais rápido possível! Agradeço a quem se dedicar a mi ajudar
-
MateusJunior
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 03, 2011 18:20
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudo
- Andamento: cursando
 por crcguilherme » Sex Mar 04, 2011 05:37
por crcguilherme » Sex Mar 04, 2011 05:37
Boa noite! esse tambem é meu primeiro post. Tai o processo de forma bem detalhada pra vc entender:
0,1 pode ser escrito assim:
![0,1 = {10}^{-1}
portanto:
{10}^{-1} = 9.10^9.\frac{(Q.Q)}{2^2}
9.10^9.\frac{Q^2}{4} = {10}^{-1}
10^9.\frac{Q^2}{4} = \frac{{10}^{-1}}{9}
10^9.Q^2 = \frac{4.{10}^{-1}}{9}
Q^2 = \frac{4.{10}^{-1}}{9.10^9}
Q^2 = \frac{4}{9}.{10}^{-1}.{10}^{-9}
Q^2 = \frac{4}{9}.{10}^{-10}
Q = \sqrt[2]{\frac{4}{9}.{10}^{-10}}
Resposta: Q = (2/3).10^{-5} 0,1 = {10}^{-1}
portanto:
{10}^{-1} = 9.10^9.\frac{(Q.Q)}{2^2}
9.10^9.\frac{Q^2}{4} = {10}^{-1}
10^9.\frac{Q^2}{4} = \frac{{10}^{-1}}{9}
10^9.Q^2 = \frac{4.{10}^{-1}}{9}
Q^2 = \frac{4.{10}^{-1}}{9.10^9}
Q^2 = \frac{4}{9}.{10}^{-1}.{10}^{-9}
Q^2 = \frac{4}{9}.{10}^{-10}
Q = \sqrt[2]{\frac{4}{9}.{10}^{-10}}
Resposta: Q = (2/3).10^{-5}](/latexrender/pictures/0a86b75f9f4eb1202aebd5714f597ddc.png)
-
crcguilherme
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mar 04, 2011 03:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por MateusJunior » Sex Mar 04, 2011 14:23
por MateusJunior » Sex Mar 04, 2011 14:23
Muito obrigado por ajudar, consegui compreender bem!
-
MateusJunior
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 03, 2011 18:20
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudo
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Física Ajudem Urgente
por Silva339 » Qua Abr 03, 2013 18:16
- 1 Respostas
- 1669 Exibições
- Última mensagem por tcornacchia

Dom Mar 16, 2014 13:15
Cálculo: Limites, Derivadas e Integrais
-
- [Fisica] Ajuda
por spektroos » Seg Set 24, 2012 01:44
- 6 Respostas
- 3153 Exibições
- Última mensagem por young_jedi

Seg Set 24, 2012 20:48
Fundamentos de Mecânica
-
- ajuda com projeto de física
por daniloadanilo » Dom Set 05, 2010 23:32
- 1 Respostas
- 3253 Exibições
- Última mensagem por Neperiano

Seg Jul 18, 2011 23:09
Desafios Fáceis
-
- [física] Ajuda Pelo amor d Deus
 por thialarcon1 » Sex Jun 13, 2008 13:59
por thialarcon1 » Sex Jun 13, 2008 13:59
- 4 Respostas
- 5225 Exibições
- Última mensagem por Neperiano

Seg Jun 18, 2012 18:11
Dúvidas Pendentes (aguardando novos colaboradores)
-
- (pêndulo-física)alguém ajuda achar energia potencial ?
por gustavoluiss » Ter Set 06, 2011 15:17
- 6 Respostas
- 3965 Exibições
- Última mensagem por gustavoluiss

Qua Set 07, 2011 01:55
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\[0,1 = 9\cdot 10^{9}\cdot \frac{Q\cdot Q}{2^{2}}\] \[0,1 = 9\cdot 10^{9}\cdot \frac{Q\cdot Q}{2^{2}}\]](/latexrender/pictures/67dcf2a856a6216affe88d93c03dedbe.png)
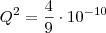


![\[0,1 = 9\cdot 10^{9}\cdot \frac{Q\cdot Q}{2^{2}}\] \[0,1 = 9\cdot 10^{9}\cdot \frac{Q\cdot Q}{2^{2}}\]](/latexrender/pictures/67dcf2a856a6216affe88d93c03dedbe.png)
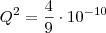


![0,1 = {10}^{-1}
portanto:
{10}^{-1} = 9.10^9.\frac{(Q.Q)}{2^2}
9.10^9.\frac{Q^2}{4} = {10}^{-1}
10^9.\frac{Q^2}{4} = \frac{{10}^{-1}}{9}
10^9.Q^2 = \frac{4.{10}^{-1}}{9}
Q^2 = \frac{4.{10}^{-1}}{9.10^9}
Q^2 = \frac{4}{9}.{10}^{-1}.{10}^{-9}
Q^2 = \frac{4}{9}.{10}^{-10}
Q = \sqrt[2]{\frac{4}{9}.{10}^{-10}}
Resposta: Q = (2/3).10^{-5} 0,1 = {10}^{-1}
portanto:
{10}^{-1} = 9.10^9.\frac{(Q.Q)}{2^2}
9.10^9.\frac{Q^2}{4} = {10}^{-1}
10^9.\frac{Q^2}{4} = \frac{{10}^{-1}}{9}
10^9.Q^2 = \frac{4.{10}^{-1}}{9}
Q^2 = \frac{4.{10}^{-1}}{9.10^9}
Q^2 = \frac{4}{9}.{10}^{-1}.{10}^{-9}
Q^2 = \frac{4}{9}.{10}^{-10}
Q = \sqrt[2]{\frac{4}{9}.{10}^{-10}}
Resposta: Q = (2/3).10^{-5}](/latexrender/pictures/0a86b75f9f4eb1202aebd5714f597ddc.png)


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.