por Renato_RJ » Ter Fev 15, 2011 00:19
por Renato_RJ » Ter Fev 15, 2011 00:19
Boa noite a todos, gostaria da correção dos colegas no desenvolvimento da questão abaixo, eu fiz, mas não sei se está certo ou se falta algum detalhe na demonstração, poderiam verificar ?
Dados
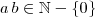
. Aplicamos sucessivamente o algoritmo de Euclides temos:
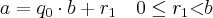
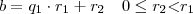
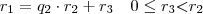

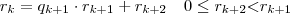
Como

. Temos que existe um primeiro inteiro s tal que
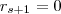
. Prove que
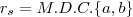
.
O que eu fiz:
Extrapolando o algoritmo temos:

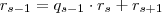
Usando o teorema abaixo:
"Se
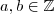
e
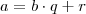
onde
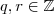
então

"
Teremos:
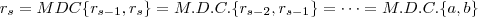
A minha demonstração está correta ? A linguagem também ?
Grato,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
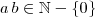 . Aplicamos sucessivamente o algoritmo de Euclides temos:
. Aplicamos sucessivamente o algoritmo de Euclides temos: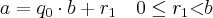
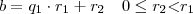
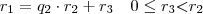

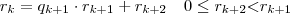
 . Temos que existe um primeiro inteiro s tal que
. Temos que existe um primeiro inteiro s tal que 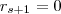 . Prove que
. Prove que 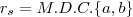 .
.
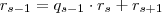
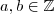 e
e 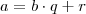 onde
onde 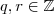 então
então  "
"