 por stanley tiago » Qui Fev 03, 2011 23:48
por stanley tiago » Qui Fev 03, 2011 23:48
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Sex Fev 04, 2011 11:40
por Elcioschin » Sex Fev 04, 2011 11:40
Você errou ao multiplicar tudo pelo MMC = x^4 - 1 = (x² - 1)*(x² + 1)
Faça novamente. No final você deve obter ----> (4x² - a² - 2)*x² = 0
Aí a resposta confere!
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por stanley tiago » Sex Fev 04, 2011 17:47
por stanley tiago » Sex Fev 04, 2011 17:47
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Sex Fev 04, 2011 18:07
por Elcioschin » Sex Fev 04, 2011 18:07
Faltou ALGO:
8x^4 - 2a²x² - 4x² = 0
Dividindo por 2 ----> 4*x^4 - a²x² - 2x² = 0
Colocando x² em evidência ----> (4x² - a² - 2)*x² = 0
Temos 2 fatores no 1º membro, logo temos as soluções
x² = 0 ----> x = 0
4x² - a² - 2 = 0 ----> 4x² = a² + 2 ----> 2x = + - \/(a² + 2) ----> x = + \/(a² + 2)/2 ou x = - \/(a² + 2)/2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por stanley tiago » Sex Fev 04, 2011 22:13
por stanley tiago » Sex Fev 04, 2011 22:13
valeu mano , muito obrigado .
mais do jeito que eu fiz tbm ta certo ?

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3152 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4145 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3423 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações
por Neperiano » Qua Fev 11, 2009 12:33
- 6 Respostas
- 6484 Exibições
- Última mensagem por marcio silva

Sex Mar 20, 2009 20:15
Sistemas de Equações
-
- Equações
por Luna » Qui Set 10, 2009 19:30
- 2 Respostas
- 2265 Exibições
- Última mensagem por Luna

Sex Set 11, 2009 19:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


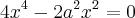

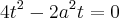
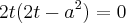

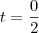

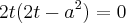
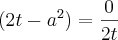




![x" =\frac{\sqrt[]{a^2}}{\sqrt[]{2}} x" =\frac{\sqrt[]{a^2}}{\sqrt[]{2}}](/latexrender/pictures/268fbeec055e3127c7bdf047fb551e6c.png)
![x" =\frac{a}{\sqrt[]{2}} x" =\frac{a}{\sqrt[]{2}}](/latexrender/pictures/c98d836f4b78378f8b4fbb41fd3be458.png)
![x" =\frac{a}{\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}} x" =\frac{a}{\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}}](/latexrender/pictures/b62d3f998a2a6dbb466f3aa8cacf7884.png)
![x" =+-\frac{a\sqrt[]{2}}{2} x" =+-\frac{a\sqrt[]{2}}{2}](/latexrender/pictures/d9cae559e10b29997be4d7236194d408.png)
![V=\left(-\frac{a\sqrt[]{2}}{2} ,0,\frac{a\sqrt[]{2}}{2} \right) V=\left(-\frac{a\sqrt[]{2}}{2} ,0,\frac{a\sqrt[]{2}}{2} \right)](/latexrender/pictures/edf05353bee2430f97b85fb6a7edf0ea.png)
![V=\left(-\frac{\sqrt[]{a^2+2}}{2} ,0,\frac{\sqrt[]{a^2+2}}{2} \right) V=\left(-\frac{\sqrt[]{a^2+2}}{2} ,0,\frac{\sqrt[]{a^2+2}}{2} \right)](/latexrender/pictures/90f691bdef4abae3196403ff9eaf163a.png)



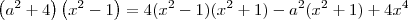

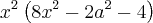
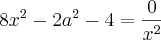

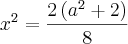
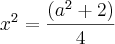
![x=\frac{\left(\sqrt[]{a^2+2 }\right)}{\sqrt[]{4}} x=\frac{\left(\sqrt[]{a^2+2 }\right)}{\sqrt[]{4}}](/latexrender/pictures/e53317be8737cdef3ac5e8c87b2522b7.png)
![x' =+-\frac{\left(\sqrt[]{a^2+2 }\right)}{2} x' =+-\frac{\left(\sqrt[]{a^2+2 }\right)}{2}](/latexrender/pictures/270d27473a3ed3e1db647b0dfd2a29f5.png)



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
