Absurdo Matemático

por **PedroSantos** » Sáb Jan 15, 2011 19:18

Seja a seguinte igualdade:

$\sqrt[]{x+2}=4-x$

Graficamente fica:

É facíl concluir por observação que só existe um ponto de intercepção.Mais tarde veremos que é o 2.
Agora resolvamos a igualdade.

$\sqrt[]{x+2}=4-x$

${(\sqrt[]{x+2})}^{2}={(4-x)}^{2}$

$x+2={(4-x)}^{2}$

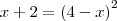
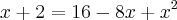
$x+2=16-8x+{x}^{2}$

$x+2-16+8x-{x}^{2}=0$

$-{x}^{2}-14+9x=0$

$-1*(-{x}^{2}+9x-14)=-1*0$

${x}^{2}-9x+14=0$

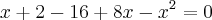
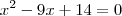
Obtemos uma função de 2º grau.

As raízes desta função são:

${x}^{2}-9x+14=0$

${x}^{2}-7x-2x+14=0$

x(x-7)-2(x-7)=0

$x-2=0 \vee x-7=0$

$x=2 \vee x=7$

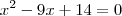
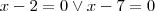
As raizes desta função são 2 e 7.Conforme se pode observar pelo gráfico.
No entanto o 7 não é solução da igualdade. Se os calculos algébricos estão corretos, a função do 2º grau deduzida a partir da igualdade deveria ter as mesmas soluções!

Porquê isto acontece?

por **MarceloFantini** » Sáb Jan 15, 2011 19:53

Isso não é um absurdo, você que não está levando em conta todas as informações: os valores tem de satisfazer a primeira igualdade, e isso significa que $4-x \geq 0 \Longrightarrow x \leq 4$ , logo, a única resposta válida é x=2

. Porque $4-x \geq 0$ ? Resposta: $\sqrt {x+2} = 4 - x$ . O resultado de uma raíz quadrada é sempre positivo.

por **PedroSantos** » Dom Jan 16, 2011 19:42

É verdade nem pensei nisso!
Obrigado

Absurdo Matemático

Absurdo Matemático

Absurdo Matemático

Re: Absurdo Matemático

Re: Absurdo Matemático

Quem está online