 por angeloka » Ter Out 19, 2010 19:10
por angeloka » Ter Out 19, 2010 19:10
1)Se a, b, c são três inteiros positivos distintos tais que

=
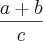
=

, qual o valor de

?
2)
a) Mostre que se b e d são inteiros positivos e

=

, então

=

.
b) Mostre que se b, d e y são inteiros positivos e

=

=

então
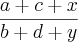
=

.
Por favor me ajude estou encontrando muita dificuldade para resolver.
-
angeloka
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Out 05, 2010 18:20
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pós em matemática
- Andamento: cursando
 por VtinxD » Ter Out 19, 2010 22:30
por VtinxD » Ter Out 19, 2010 22:30
1)

(1)=
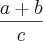
(2)=

(3)
Multiplicando (1) e (2) em cruz:

Sendo
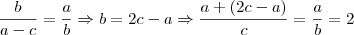
Tenho que ir dormir agora mas espero ter ajudado pelo menos com essa ai hehe...
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por VtinxD » Ter Out 19, 2010 23:07
por VtinxD » Ter Out 19, 2010 23:07
Foi mal mas não consegui resistir ao desejo....

:
2)a)Como
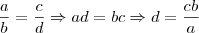
e
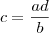
Agora sendo x oque queremos descobrir:

e substituindo as equações acima nessa temos:

,tirando o mmc

Repetindo o de cima e multiplicando pelo de baixo:
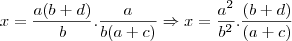
Como

,

A 2-b) é só repetir a 2-a) e que da pra chegar lá.Boa noite e espero ter ajudado
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por fernandesdejesus » Sáb Out 23, 2010 02:09
por fernandesdejesus » Sáb Out 23, 2010 02:09
Mostre que se b, d e y são inteiros positivos e a/b = c/d = x/y então (a + c + x) / (b + d +y) = x/y
(a+c+x)/(b+d+y)= x/y ? y(a+c+x)=x(b+d+y) ? (a+c+x)=(xb+xd+xy)/y ?
a+c +x=xb/y+ xd/y+ xy/y ? a+c + x=xb/y+ xd/y+ x ? a+c + x -x=xb/y+ xd/y ?
a+c = xb/y+ xd/y ? a+c = (x(b+d))/y ? (a+c)/(b+d) = x/y
Tomamos z= x/y , então z = (a+c)/(b+d)
a/b = c/d ? a.d=c.b ? d=(c.b)/a e c=(a.d)/b
Substituindo as equações acima nesta atual z = (a+c)/(b+d), temos z = (a+ad/b)/(b+cb/a) ? então:
Z = (ab+ad)/b ÷ (ab+cb)/a ? z = (a(b+d))/b ÷ (b(a+c))/a ? z = (a(b+d))/b × a/(b(a+c)) ? z = (a²(b+d))/(b²(a+c))
z = = a²/b² × (b+d)/(a+c) ?
Se (a+c)/(b+d) =z , então o inverso da fração (b+d)/(a+c) = 1/z ?
Substituindo então 1/z, temos:
z = a²/b² × 1/z ? z² = a²/b² ? z = ?(a²/b²) ? z = a/b. Sendo z = x/y, temos então x/y = a/b = c/d
-
fernandesdejesus
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Out 23, 2010 02:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: especialização em matemática
- Andamento: cursando
 por angeloka » Sáb Out 23, 2010 17:06
por angeloka » Sáb Out 23, 2010 17:06
muito obrigada quebrei muito a cabeça hoje tentando resolver este, da metade do exercício não conseguia sair, valeu mesmo.
-
angeloka
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Out 05, 2010 18:20
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pós em matemática
- Andamento: cursando
 por Carlos » Dom Out 24, 2010 16:27
por Carlos » Dom Out 24, 2010 16:27
Angeloca estou fazendo o mesmo curso que você, podria enviar-me seu e-mail para fazermos contatos segue o meu taambém estou precisando de ajuda .
Um grande abraço
Carlos
email:
caooliver@ig.com.br
-
Carlos
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Out 24, 2010 10:04
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por angeloka » Dom Out 24, 2010 19:41
por angeloka » Dom Out 24, 2010 19:41
oi sou Angela, olha estou com muitas dificuldades se não fosse este fórum nem sei o que seria, mas vamos ver o que vai dar, o meu e mail é
meloangela90@yahoo.com.br
-
angeloka
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Out 05, 2010 18:20
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: pós em matemática
- Andamento: cursando
 por ktarrento » Dom Out 24, 2010 23:19
por ktarrento » Dom Out 24, 2010 23:19
Valeu pela ajuda estava encontrando dificuldade em terminar lição de casa, valeu agora vou estudar. Tenham uma boa noite e uma boa semana.

-
ktarrento
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 24, 2010 22:41
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenciatura Matemática
- Andamento: cursando
 por Eddie » Ter Out 26, 2010 14:02
por Eddie » Ter Out 26, 2010 14:02
Angeloka, acredito q esteja fazendo o mesmo curso q vc, caso te interesse podemos nos ajudar, passando exercicios e resultados, eu não consegui resolver os de indulção, caso vc tenha conseguido, vc pode me dar uma força? obrigado
-
Eddie
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Out 23, 2010 10:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aritmética, geometrias de posição e métrica e razões trigono
 por angeloka » Sex Dez 03, 2010 18:26
por angeloka » Sex Dez 03, 2010 18:26
- 1 Respostas
- 1640 Exibições
- Última mensagem por angeloka

Sex Dez 03, 2010 22:16
Trigonometria
-
- Aritmética, Geometrias de Posição e Métrica, Razões Trigonom
 por angeloka » Sex Nov 26, 2010 22:55
por angeloka » Sex Nov 26, 2010 22:55
- 4 Respostas
- 3223 Exibições
- Última mensagem por fttofolo

Seg Nov 29, 2010 00:02
Álgebra Elementar
-
- [Média Aritmética] Razões, Proporções e Regra de Três
por Tatasacchi_123 » Ter Mar 26, 2013 16:24
- 2 Respostas
- 5522 Exibições
- Última mensagem por Tatasacchi_123

Qua Mar 27, 2013 17:37
Sistemas de Equações
-
- Geometria Métrica
por von grap » Ter Abr 26, 2011 16:51
- 1 Respostas
- 1567 Exibições
- Última mensagem por guillcn

Ter Abr 26, 2011 18:01
Geometria Espacial
-
- geometria métrica e espacial
 por Aquamarine » Sáb Fev 11, 2012 16:15
por Aquamarine » Sáb Fev 11, 2012 16:15
- 3 Respostas
- 2466 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 11, 2012 21:00
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 =
=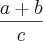 =
= , qual o valor de
, qual o valor de  ?
? =
= , então
, então =
= .
. =
= =
= então
então 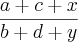 =
= .
.
 =
=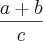 =
= , qual o valor de
, qual o valor de  ?
? =
= , então
, então =
= .
. =
= =
= então
então 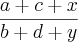 =
= .
.
 (1)=
(1)=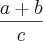 (2)=
(2)= (3)
(3)
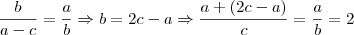

 :
: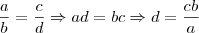 e
e 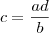
 e substituindo as equações acima nessa temos:
e substituindo as equações acima nessa temos: ,tirando o mmc
,tirando o mmc 
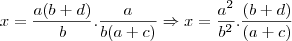
 ,
,







