-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478016 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530573 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 494162 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 702208 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2115128 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por flavio2010 » Dom Jul 11, 2010 10:03
por flavio2010 » Dom Jul 11, 2010 10:03
Seja p(x)=x^2+px+p uma função real na variável real.Os valores de p para os quais f(x)=0 possue raiz dupla positiva são:
a) 0<p<4
b) p=4
c) p=0
d) f(x)=0 não pode ter raiz dupla positiva
e) n.r.a
-
flavio2010
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jun 10, 2010 22:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Douglasm » Dom Jul 11, 2010 10:44
por Douglasm » Dom Jul 11, 2010 10:44
Primeiramente, para que haja raiz dupla, o discriminante deve ser nulo:
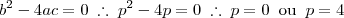
Para p = 0, nós temos o próprio zero como raiz dupla, que não é o que nós queremos, pois a raiz deve ser dupla e positiva. Para p = 4, nós teremos -2 como raiz dupla, o que também não nos serve. Consequentemente a resposta é letra D.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Tom » Dom Jul 11, 2010 16:00
por Tom » Dom Jul 11, 2010 16:00
Em concordância com o que ja foi explanado, segue abaixo outras resoluções:
Resolução 1:
Seja

um polinômio tal que
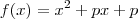
. Seja

a raiz dupla de

, então a primeira derivada de

no ponto

é nula, isto é:
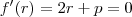
, assim
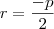
é a raiz dupla.
Além disso Se

é raiz, então:
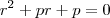
, isto é,
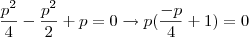
e como
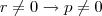
e decore em

.
Resolução 2:Seja

um polinômio ta que
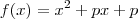
. Seja

a raiz dupla de

, pelas relações de Girard, temos:

e
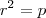
e dessas obtemos:
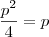
e como
 Resolução 3:
Resolução 3:Se

adimite raiz dupla e é um polinômio do segundo grau, então

pode ser reduzido a um quadrado perfeito de forma canônica:
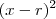
, tal que

é sua raiz. Assim,
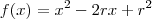
. Fazendo a identidade polinomial entre o polinômio supracitado e o fornecido pelo enunciado, obtemos:
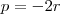
e

e dessas relalçõs surge:
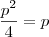
e como

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Condição de Existência
por gustavowelp » Sáb Jun 26, 2010 11:56
- 5 Respostas
- 5025 Exibições
- Última mensagem por Molina

Sáb Jun 26, 2010 20:49
Logaritmos
-
- Provar a existência de subespaços
por valeuleo » Seg Set 19, 2011 10:52
- 2 Respostas
- 1508 Exibições
- Última mensagem por valeuleo

Seg Set 19, 2011 12:19
Álgebra Linear
-
- Demonstração de existencia de subespaço
por leandro_aur » Dom Mar 04, 2012 19:29
- 0 Respostas
- 1166 Exibições
- Última mensagem por leandro_aur

Dom Mar 04, 2012 19:29
Introdução à Álgebra Linear
-
- [Limite] Conceito de Existência
por eli83 » Qua Out 10, 2012 10:33
- 4 Respostas
- 2162 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Teorema de Existencia e Unicidade
por Crist » Sex Mar 15, 2013 21:07
- 0 Respostas
- 1105 Exibições
- Última mensagem por Crist

Sex Mar 15, 2013 21:07
Equações Diferenciais Ordinárias e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 22 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



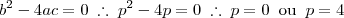

 um polinômio tal que
um polinômio tal que 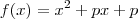 . Seja
. Seja  a raiz dupla de
a raiz dupla de  , então a primeira derivada de
, então a primeira derivada de  no ponto
no ponto  é nula, isto é:
é nula, isto é: 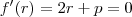 , assim
, assim 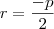 é a raiz dupla.
é a raiz dupla. é raiz, então:
é raiz, então: 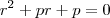 , isto é,
, isto é, 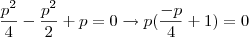 e como
e como 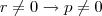 e decore em
e decore em  .
. um polinômio ta que
um polinômio ta que 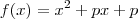 . Seja
. Seja  a raiz dupla de
a raiz dupla de  , pelas relações de Girard, temos:
, pelas relações de Girard, temos: e
e 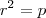 e dessas obtemos:
e dessas obtemos: 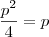 e como
e como 
 adimite raiz dupla e é um polinômio do segundo grau, então
adimite raiz dupla e é um polinômio do segundo grau, então  pode ser reduzido a um quadrado perfeito de forma canônica:
pode ser reduzido a um quadrado perfeito de forma canônica: 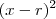 , tal que
, tal que  é sua raiz. Assim,
é sua raiz. Assim, 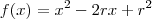 . Fazendo a identidade polinomial entre o polinômio supracitado e o fornecido pelo enunciado, obtemos:
. Fazendo a identidade polinomial entre o polinômio supracitado e o fornecido pelo enunciado, obtemos: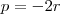 e
e  e dessas relalçõs surge:
e dessas relalçõs surge: 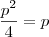 e como
e como 

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.