Os pontos equidistantes dos eixos coordenados e, ao mesmo tempo, equidistantes dos pontos P(1,2) e Q(-3,4) são os extremos de segmento de comprimento igual a:
a) 10V5/3
b) 10V5
c) 5V5
d) 5V5/5
e) 10



 .
. e
e  , decorre da equação para distância entre pontos:
, decorre da equação para distância entre pontos: 
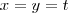 , então:
, então:  e, portanto,
e, portanto,  e, nesse caso, o ponto em questão tem coordenada
e, nesse caso, o ponto em questão tem coordenada 
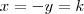 , então:
, então: 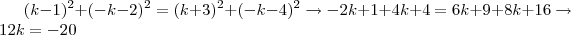 e, nesse caso, o ponto em questão tem coordenada:
e, nesse caso, o ponto em questão tem coordenada:
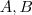 :
: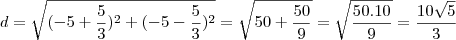

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: