 por jones_slash » Seg Jun 07, 2010 22:49
por jones_slash » Seg Jun 07, 2010 22:49
Como posso mostrar q 13 elevado a 3n + 17 elevado a 3n é múltiplo
de 45 para todo n E N ímpar??
-
jones_slash
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jun 05, 2010 17:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletrotecnica e eletronica
- Andamento: formado
 por davi_11 » Ter Jun 08, 2010 14:22
por davi_11 » Ter Jun 08, 2010 14:22
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
 por davi_11 » Qui Jun 10, 2010 14:12
por davi_11 » Qui Jun 10, 2010 14:12
Cometi um equivoco na ultima linha e peço mil desculpas, na verdade confundi as propriedades.
Talvez de para se provar usando indução sobre n.
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



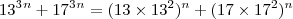
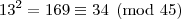


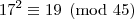
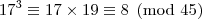
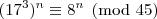
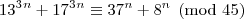
 divide 45, então
divide 45, então  também divide.
também divide.



 .
.
 :
: