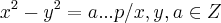 ,mostre que a é impar.
,mostre que a é impar.soluçao:
para q. a equaçao tenha soluçao teremos q. ter:
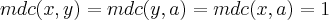 ,ou seja:
,ou seja:primos dois a dois...logo,nao poderemos ter ambos
 pares.
pares.e nem ambos impares,pois:se forem pares mdc(x,y) sera multiplo de 2 e refuta a condiçao de soluçao.se forem impares teriamos:
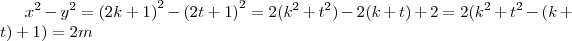 ,q ´um numero par,e portanto divisivel por 2,o q. refuta a condiçao(mdc(x,y)=1) de termos soluçoes inteiras p. a equaçao diofantina dada.portanto a ,somente podera ser impar.
,q ´um numero par,e portanto divisivel por 2,o q. refuta a condiçao(mdc(x,y)=1) de termos soluçoes inteiras p. a equaçao diofantina dada.portanto a ,somente podera ser impar.ou entao,
 tem q. ser um par,outro impar.entao:
tem q. ser um par,outro impar.entao:suporemos x,impar e y,par,logo:
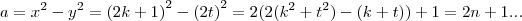
raciocinio analogo p/
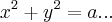


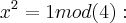 ,x impar.
,x impar. 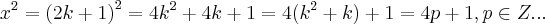 ,ou seja:
,ou seja: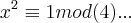 ,entao:
,entao: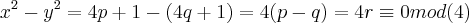 q. contradiz a condiçao exposta acima...
q. contradiz a condiçao exposta acima... é tbem um impar quadrado,ou seja:
é tbem um impar quadrado,ou seja: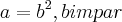
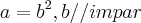 ...
...
 .
.



