Olá.
A resoluções serão enviadas em seguida, mas devo esclarecer o seguinte:
Atualmente não resolvemos listas de exercícios.
Mesmo que seja apenas um exercício, pedimos para que não seja enviado o enunciado somente, pois queremos interagir com as tentativas de resolução dos participantes, entender as dificuldades e dar dicas com o intuito de esclarecer algumas dúvidas para que a resolução seja alcançada pelo(a) estudante.
Também porque, até o momento, infelizmente não temos outros colaboradores ativos nas ajudas.
Este é um trabalho voluntário e assim acreditamos que haverá uma real Ajuda Matemática.
Caso não seja possível a participação direta de sua filha no fórum, tente compartilhar suas tentativas e dúvidas e tentaremos aos poucos ajudar.
Em uma barraca de caldo de cana, são vendidos 2 tamanhos de copos, um de 250 ml e outro de 500 ml. O preço do copo pequeno é R$ 1,00, e o do médio, R$ 1,50. Se comprei, no total, 2 litros de caldo de cana e paguei R$ 6,50, quantos copos pequenos e quantos copos médios comprei?
O enunciado fornece dados para representarmos um sistema com duas equações e duas incógnitas.
Nomeando as variáveis:

: quantidade comprada de copos pequenos

: quantidade comprada de copos médios

Da segunda equação, obtemos:
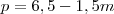
Substituindo

na primeira equação:

Simplificando, dividindo os dois membros por 250:




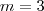
unidades de copos médios
Substituindo

obtido na segunda equação, por exemplo:

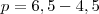

unidades de copos pequenos
OUTRA:uMA CIRCUNFERÊNCIA TEM CUMPRIMENTO IGUAL A 20 PI cm. Qual o perímetro de um decágono regular com lado igual ao raio desta circunferência?
Com a informação de que uma circunferência tem comprimento C igual a

cm, podemos descobrir o raio r, pois:


Dividindo os dois membros da equação por

:
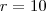
cm
Um decágono regular possui 10 lados de mesma medida. E o perímetro

é a soma das medidas dos lados, então:



cm
outra:Se há 5 anos a soma das idades de Ricardo e Renato era 40 anos, qual é a soma das idades de Ricardo e Renato hoje?
Apenas precisamos representar a soma das idades no passado.

: idade atual de Ricardo

: idade atual de Renato
Soma das idades no passado:

Calculando

que é a soma no presente:

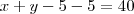

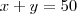
outra:Somando dois números pares consecutivos, obtemos 138. Sabendo disso, quanto vale o produto entre eles?
Um número par é um número da forma

, onde

é um natural não nulo (1, 2, 3, ...).
Então, a soma dos dois números pares consecutivos é:

Agora, podemos calcular

:

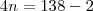


Logo, os números são:
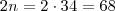
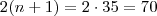
O produto pedido:
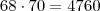
última:Uma padaria fabrica dois tipos de pão. Dois terços dos clientes preferem pães sem gergelim, e o restante, com gergelim. Depois de uma campanha de degustação, ¼ dos compradores que preferiam pães sem gergelim passaram a comprar do outro tipo de pão. Qual a fração dos compradores que prefere, agora, pães com gergelim? O resultado deve ser uma fração irredutível.
Como são apenas dois tipos de pão, se

dos clientes preferem pães
sem gergelim, o restante citado equivale a

dos clientes (aqueles que preferem pães
com gergelim antes da campanha), pois a soma das frações precisa ser 1 (todos os clientes).
Então, já sabemos que antes da campanha, os que preferem pães
com gergelim representam

dos clientes.
À esta fração, após a campanha, devemos somar

de

.
Fração de clientes que atualmente preferem pães
com gergelim:
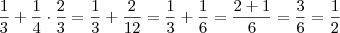
Ou seja, após a campanha, a preferência por pães
com gergelim subiu de

para a metade dos clientes.
Mauro, espero ter ajudado e agradeço sua compreensão!


 : quantidade comprada de copos pequenos
: quantidade comprada de copos pequenos : quantidade comprada de copos médios
: quantidade comprada de copos médios
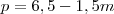





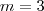 unidades de copos médios
unidades de copos médios
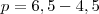
 unidades de copos pequenos
unidades de copos pequenos cm, podemos descobrir o raio r, pois:
cm, podemos descobrir o raio r, pois:

 :
: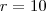 cm
cm é a soma das medidas dos lados, então:
é a soma das medidas dos lados, então:

 cm
cm : idade atual de Ricardo
: idade atual de Ricardo : idade atual de Renato
: idade atual de Renato
 que é a soma no presente:
que é a soma no presente:
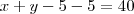

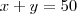
 , onde
, onde  é um natural não nulo (1, 2, 3, ...).
é um natural não nulo (1, 2, 3, ...).

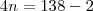


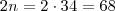
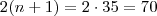
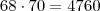
 dos clientes preferem pães
dos clientes preferem pães  dos clientes (aqueles que preferem pães
dos clientes (aqueles que preferem pães  de
de 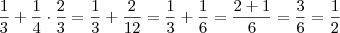

![\left(\sqrt[2]{2+\sqrt[2]{3}}\right)\prime2 \left(\sqrt[2]{2+\sqrt[2]{3}}\right)\prime2](/latexrender/pictures/d9296aa1a10e393e66951e95370d86a7.png) ou
ou ![\left(\sqrt[2]{6}+\sqrt[2]{3}\right)\prime4 \left(\sqrt[2]{6}+\sqrt[2]{3}\right)\prime4](/latexrender/pictures/7f17fa2431e2b8517b15b69e2f3a9a07.png) ?
?![\sqrt[2]{7+4\sqrt[2]{3}}+\sqrt[2]{7-4\sqrt[2]{3}} \sqrt[2]{7+4\sqrt[2]{3}}+\sqrt[2]{7-4\sqrt[2]{3}}](/latexrender/pictures/1317fc02ded226d8050b1a0e8cf6ab1b.png) é racional(sugestão calcule x^2)
é racional(sugestão calcule x^2)![{\left(\sqrt[2]{7+4\sqrt[2]{3}} \right)}^{2}+{\left(\sqrt[2]{7-4\sqrt[2]{3}} \right)}^{2} {\left(\sqrt[2]{7+4\sqrt[2]{3}} \right)}^{2}+{\left(\sqrt[2]{7-4\sqrt[2]{3}} \right)}^{2}](/latexrender/pictures/8cf34815a2571e27a18c2581a822bfa6.png)
![7+4\sqrt[2]{3}+7-4\sqrt[2]{3} 7+4\sqrt[2]{3}+7-4\sqrt[2]{3}](/latexrender/pictures/69d194492e50637c2c2099ed6db89061.png)
![\sqrt[2]{14} \sqrt[2]{14}](/latexrender/pictures/39330cac5cba7044ed7dbd9b942ed5e1.png)