-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480045 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 538129 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501915 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 723382 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2157566 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Larissa Ferreira » Sex Fev 17, 2017 15:12
por Larissa Ferreira » Sex Fev 17, 2017 15:12
Não consigo chegar a uma conclusão na demonstração de que todo subgrupo de um grupo ciclico é ciclico, e que U é normal de G
-
Larissa Ferreira
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Fev 17, 2017 10:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matematica
- Andamento: cursando
 por adauto martins » Sáb Fev 18, 2017 11:35
por adauto martins » Sáb Fev 18, 2017 11:35
seja
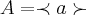
um grupo gerador ciclico e
![B \subseteq A,[e]\neq B B \subseteq A,[e]\neq B](/latexrender/pictures/f063d0a3402343d4b4a4c1462f4e330a.png)
,B um subgrupo de A...
logo,
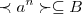
,seja

tal q.

,logo existem
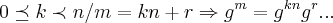

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Subgrupo cíclico e normal
por EANDRIOLI » Qua Ago 06, 2014 23:44
- 1 Respostas
- 1322 Exibições
- Última mensagem por adauto martins

Qui Nov 27, 2014 12:27
Álgebra Elementar
-
- Subgrupo normal e numero primo
por EANDRIOLI » Qua Ago 06, 2014 23:47
- 1 Respostas
- 1664 Exibições
- Última mensagem por adauto martins

Qui Nov 27, 2014 12:13
Álgebra Elementar
-
- demonstração de grupo e subgrupo
por marinho » Sex Nov 30, 2012 15:45
- 0 Respostas
- 1117 Exibições
- Última mensagem por marinho

Sex Nov 30, 2012 15:45
Álgebra Elementar
-
- [Distribuição normal] com normal reduzida e tabela, dúvida
 por MarciaChiquete » Sáb Set 17, 2016 20:38
por MarciaChiquete » Sáb Set 17, 2016 20:38
- 0 Respostas
- 7735 Exibições
- Última mensagem por MarciaChiquete

Sáb Set 17, 2016 20:38
Estatística
-
- Grupo e subgrupo
por matmatco » Sáb Out 05, 2013 17:32
- 1 Respostas
- 1156 Exibições
- Última mensagem por Bravim

Sáb Out 05, 2013 20:52
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



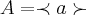 um grupo gerador ciclico e
um grupo gerador ciclico e ![B \subseteq A,[e]\neq B B \subseteq A,[e]\neq B](/latexrender/pictures/f063d0a3402343d4b4a4c1462f4e330a.png) ,B um subgrupo de A...
,B um subgrupo de A...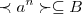 ,seja
,seja  tal q.
tal q.  ,logo existem
,logo existem 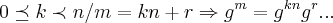


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.