Bem, não sei onde deveria postar isso, é uma dúvida em uma questão de Calculo I, mas é uma dúvida básica de decidir postar aqui. Peço perdão se estiver equivocado
- A questão pede para construir o gráfico da seguinte função.
f(x) = 3x? + 4x³ - 36x² + 29
e estou com dificuldades para achar as raízes onde x= 0
por indução eu descobri que umas das raízes é X¹=1, basta substituir e verificar. Dividindo por ( x -1 ) é o obtido a função --> g(x) = 3x³ + 7x² - 29x - 29. Se eu achar as 3 desse eu consigo resolver.
R=As outras raízes que verifiquei com um software de gráfico são -> X²(-0.88,0) X³(2.66,0) X?(-4.11,0)


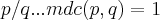 ,onde
,onde  e
e  ...entao o conj. da possivel ou possiveis raizes racionais saira do conj.{
...entao o conj. da possivel ou possiveis raizes racionais saira do conj.{ }...o intervalo onde essas raizes estarao e dado por:
}...o intervalo onde essas raizes estarao e dado por: ,q. no nosso caso sera
,q. no nosso caso sera ![\rho =1+ 36/3=13\Rightarrow {I}_{s}=[-13,13] \rho =1+ 36/3=13\Rightarrow {I}_{s}=[-13,13]](/latexrender/pictures/16a708bb807494ceacfe6500e78a82c6.png) ,ou seja todos os possiveis num. do conj. podem ser raiz do polinomio...como vc verificou q. 1 é raiz ou seja
,ou seja todos os possiveis num. do conj. podem ser raiz do polinomio...como vc verificou q. 1 é raiz ou seja 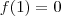 e fatorou em
e fatorou em  ...agora fazer o mesmo processo com
...agora fazer o mesmo processo com  ,pois
,pois  ,ai vai baixando grau do polinomio,q. é quarto grau,foi pra terceiro e assim sucessivamente...esse polinomio
,ai vai baixando grau do polinomio,q. é quarto grau,foi pra terceiro e assim sucessivamente...esse polinomio 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)