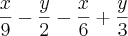por Sarah_bernadeth » Sex Mar 28, 2008 18:47
Ola pessoal.
Curso o 8º ano do ensino medio, tenho um exercíco para entregar, porem tenho muitas duvidas...
Ai vão algumas delas:
b) 3a-6a-
+1 c)
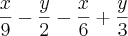d)
Minhas duvidas:
b) não consiguo resolver o numero sempre da positivo, e o resultado é negativo, e quando resolvo esta 10 numeros a mais ou a menos do resultado.
c) o MMC q estou fazendo da 9 e quando vou dividir e depois multiplicar da um numero fracionado e torna a questão ainda mais dificil.
d)o resultado sempre da uma fração q esta 25 ou 30 numeros do resultado correto.
Por favor me ajudem, presciso muito de ajuda meu professor ensina mal, e o livro não é grande coisa.
-
Sarah_bernadeth
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Sex Mar 28, 2008 18:24
- Área/Curso: Estudante
- Andamento: cursando
por admin » Sex Mar 28, 2008 20:02
Olá Sarah_bernadeth, seja bem-vinda!
Que bom que especificou algumas de suas dúvidas, isso é importante.
Entretanto, lendo apenas o que você colocou, não há propósito no exercício, ou seja, é necessário informar também o que se pede exatamente.
Favor incluir o enunciado do problema e tentaremos ajudá-la!
Até mais.
-
admin
- Colaborador Administrador - Professor
-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Tenho dúvidas de como resolver este exercício de conjuntos
por Thiago Sousa » Ter Mai 06, 2008 17:11
- 2 Respostas
- 4450 Exibições
- Última mensagem por Thiago Sousa
Ter Mai 06, 2008 19:25
Conjuntos
-
- Resolver um problema que tenho duvidas
por amanda s » Dom Nov 17, 2013 16:39
- 2 Respostas
- 1868 Exibições
- Última mensagem por amanda s
Dom Nov 17, 2013 20:39
Cálculo: Limites, Derivadas e Integrais
-
- como resolver este exercicios
por leosoares » Qui Set 09, 2010 12:29
- 2 Respostas
- 4129 Exibições
- Última mensagem por LEANDRO HENRIQUE
Ter Ago 20, 2013 11:55
Pedidos
-
- COMO RESOLVER ESTE EXERCICIOS
por LEANDRO HENRIQUE » Dom Ago 18, 2013 17:38
- 0 Respostas
- 3941 Exibições
- Última mensagem por LEANDRO HENRIQUE
Dom Ago 18, 2013 17:38
Polinômios
-
- [Termodinâmica] como resolver este problema?
por hugo82 » Qui Nov 17, 2011 09:21
- 7 Respostas
- 6270 Exibições
- Última mensagem por hugo82
Sex Nov 18, 2011 07:32
Termodinâmica I
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
