 por pkutwak » Ter Mar 02, 2010 18:13
por pkutwak » Ter Mar 02, 2010 18:13
Nunca usei, mas hoje quando fui resolver alguns exercícios de regra de três, deparei-me com uma conversão de horas.
Vi que não lembro mais nada sobre como somar ou subtrair horas minutos e segundos.
Por exemplo: 1h 45 minutos e 52 segundos + 2h 27 minutos e 18 segundos.
Alguém tem algum local onde posse ler sobre o assunto? Unica cois que lembrei, se passar de 60 minutos passar para outra unidade.
Obrigado.
-
pkutwak
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Ter Fev 23, 2010 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Molina » Ter Mar 02, 2010 18:49
por Molina » Ter Mar 02, 2010 18:49
Boa tarde.
É como fazer uma soma normal. Só que quando os segundos chegar ao 60 você 'zera' ele, colocando apenas o valor que passou de 60 e adiciona 1 minuto nos algarismos dos minutos. Mesma coisa é feito com o algarismo do minuto se passar do 60, só que você adiciona 1h nos algarismos das horas.
Por exemplo:
Numa soma convencional,

, pois:
15
1732
Note que 5 + 7 não dá 2, e sim 12, só como passou de 10 eu coloco apenas o algarismo da unidade e adiciono 1 no algarismo da dezena. O mesmo procedimento é feito para soma de tempo, veja:
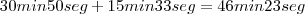
, pois:
30min50seg
15min33seg46min23seg
Perceba que 50 + 33 não dá 23, e sim 83, só que como passou de 60, eu uso apenas este valor que passou, no caso, 23. E adicionei 1 minuto na casa dos minutos.
Ajudou?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por pkutwak » Ter Mar 02, 2010 20:37
por pkutwak » Ter Mar 02, 2010 20:37
Está ótimo, agora entendi, a subtração creio eu, deve ser a mesma coisa.
-
pkutwak
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Ter Fev 23, 2010 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Molina » Ter Mar 02, 2010 22:00
por Molina » Ter Mar 02, 2010 22:00
pkutwak escreveu:Está ótimo, agora entendi, a subtração creio eu, deve ser a mesma coisa.
Isso mesmo. Só que nos casos de 'pegar emprestado', você vai pegar 60 segundos ou 60 minutos. Por exemplo, essa subtração:
13min15seg
07min30seg05min45seg
Note que eu 'peguei emprestado' 60 segundos do 13min, ficando com 75 segundos. Subtraindo 30, fico com 45 segundos. E não tenho mais 13 min e sim 12 min (já que eu emprestei 60 seg que é igual a 1 minuto).
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- porcentagem de minutos
por MariliaCS » Sex Mar 06, 2015 22:07
- 2 Respostas
- 4434 Exibições
- Última mensagem por MariliaCS

Sáb Mar 07, 2015 13:00
Álgebra Elementar
-
- [Distribuição de Poisson] problemas com minutos
por luiz_henriquear » Sáb Jun 02, 2012 16:26
- 1 Respostas
- 2029 Exibições
- Última mensagem por Neperiano

Ter Jun 05, 2012 18:39
Probabilidade
-
- Percentagem de horas
 por pegr » Sáb Jun 08, 2013 01:09
por pegr » Sáb Jun 08, 2013 01:09
- 0 Respostas
- 1305 Exibições
- Última mensagem por pegr

Sáb Jun 08, 2013 01:09
Estatística
-
- tem horas q eu to tentando resolver :/
por Amandatkm » Qui Mai 02, 2013 18:36
- 13 Respostas
- 7477 Exibições
- Última mensagem por e8group

Dom Mai 05, 2013 14:23
Equações
-
- Problema do Navegador e as horas
por zenildo » Seg Mai 02, 2016 13:18
- 1 Respostas
- 1809 Exibições
- Última mensagem por nakagumahissao

Qua Mai 04, 2016 08:45
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , pois:
, pois: , pois:
, pois:


 , avisa que eu resolvo.
, avisa que eu resolvo.

