-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478057 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530829 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 494418 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 702960 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2116442 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por BrenoNaval » Dom Abr 13, 2014 22:06
por BrenoNaval » Dom Abr 13, 2014 22:06
(MIT-HARVARD) Sendo .: X#Y=
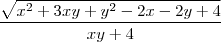
Ache o valor de ((...((2007#2006)#2005)#...)#1)
Essa questão é do livro praticando aritmética do lacerda,no entanto envolve mais álgebra e sequência lógica. Neste capítulo de operações internas é possível notar que em todos os exercícios o objetivo é encontrar uma sequência,no entanto esse exercício me tirou do sério,pois tentei de tudo e todos os possíveis produtos notáveis existentes nessa expressão.Estudo no curso apogeu um dos cursos com maiores índices de aprovação do brasil,com isso posso dizer do grau de dificuldade dessa questão ,pois nem meu professor de aritmética conseguiu resolver.Espero que alguém posso me ajudar,e caso isso venha acontecer,saiba amigo que você é um gênio

-
BrenoNaval
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mar 30, 2014 19:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Abr 14, 2014 01:33
por e8group » Seg Abr 14, 2014 01:33
Fixe

, e avaliaremos
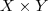
, para certos valores de Y , conforme sua definição :

(1)
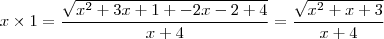
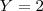
(2)
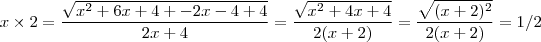
se

.
Agora segue a seguinte observação :
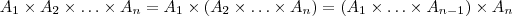
. Para infinitos termos também vale, desde que a convergência fique bem claro ..
Ora ,
![( \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 \times 2 ) \times 1 =
[tex] ([ \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 ] \times 2 ) \times 1 ( \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 \times 2 ) \times 1 =
[tex] ([ \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 ] \times 2 ) \times 1](/latexrender/pictures/fafc46b01dcd24d5c63f9ae9d93b4487.png)
.
Se admitimos que a expressão entre colchetes é convergente para um número maior que -2 , poderemos utilizar a relação (2) que diz que
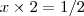
sempre que
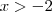
.
Daí , esta expressão
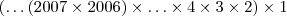
se resume a

..Só fazer as contas utilizando a definição de
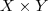
.
P.S.: O simbolo

neste contexto não és multiplicação entre dois números .
Aqui em MG onde eu moro há um Apogeu , dizem que é bom mesmo ..
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Será que algum gênio resolve isso?
por BrenoNaval » Dom Mar 30, 2014 19:27
- 4 Respostas
- 4846 Exibições
- Última mensagem por BrenoNaval

Sex Abr 11, 2014 12:02
Aritmética
-
- [Álgebra elementar] Como isso é chamado?
por GandalfOBranco » Dom Jul 17, 2016 00:55
- 8 Respostas
- 11852 Exibições
- Última mensagem por GandalfOBranco

Qua Abr 12, 2017 21:04
Álgebra Elementar
-
- Consegue resolver o limite?
por Cleyson007 » Sáb Abr 28, 2012 17:18
- 1 Respostas
- 1107 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 14:59
Cálculo: Limites, Derivadas e Integrais
-
- Alguem consegue resolver esse limite?
por priscila1992 » Dom Abr 15, 2012 17:26
- 1 Respostas
- 1275 Exibições
- Última mensagem por LuizAquino

Seg Abr 16, 2012 15:09
Cálculo: Limites, Derivadas e Integrais
-
- [Equação exponencial] Alguém consegue resolver?
por riickscrotzze » Ter Jun 04, 2013 15:55
- 5 Respostas
- 5640 Exibições
- Última mensagem por riickscrotzze

Qua Jun 05, 2013 13:53
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 17 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
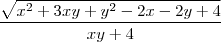


 , e avaliaremos
, e avaliaremos 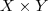 , para certos valores de Y , conforme sua definição :
, para certos valores de Y , conforme sua definição : 
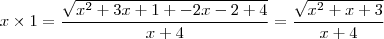
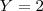
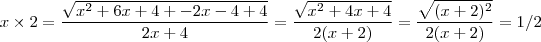 se
se  .
. 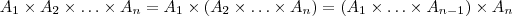 . Para infinitos termos também vale, desde que a convergência fique bem claro ..
. Para infinitos termos também vale, desde que a convergência fique bem claro .. ![( \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 \times 2 ) \times 1 =
[tex] ([ \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 ] \times 2 ) \times 1 ( \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 \times 2 ) \times 1 =
[tex] ([ \hdots (2007 \times 2006) \times \hdots \times 4 \times 3 ] \times 2 ) \times 1](/latexrender/pictures/fafc46b01dcd24d5c63f9ae9d93b4487.png) .
.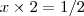 sempre que
sempre que 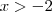 .
. 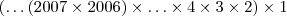 se resume a
se resume a  ..Só fazer as contas utilizando a definição de
..Só fazer as contas utilizando a definição de  neste contexto não és multiplicação entre dois números .
neste contexto não és multiplicação entre dois números .





