 por marinalcd » Qui Mar 06, 2014 16:37
por marinalcd » Qui Mar 06, 2014 16:37
Estou ajudando um colega e ele me apresentou este desafio que não conseguiu resolver:
Mostre que os anéis
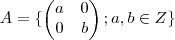
e
![B = Z[\sqrt[]{2}] = \{ a + b\sqrt[]{2} ; a,b \in Z\} B = Z[\sqrt[]{2}] = \{ a + b\sqrt[]{2} ; a,b \in Z\}](/latexrender/pictures/5dc859b87cd069ea4fd87390c50b3fbe.png)
não são isomorfos.
A dica é supor um homomorfismo
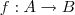
e mostrar que
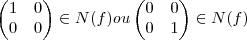
.
Tentei provar que N(f) não é injetora, mas não estou conseguindo resolver este desafio.
Alguém pode me ajudar?
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por adauto martins » Sex Dez 05, 2014 17:25
por adauto martins » Sex Dez 05, 2014 17:25
A={
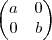
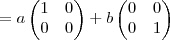
,
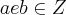
}
vamos tomar

seja um homomorfismo,f(x)=y,onde
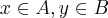
...logo teremos
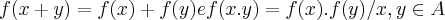
f(
![(\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
c & 0 \\
0 & d
\end{pmatrix})=f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & c.d
\end{pmatrix})=
(a.c+0\sqrt[]{2}).(0+c.d\sqrt[]{2}) (\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
c & 0 \\
0 & d
\end{pmatrix})=f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & c.d
\end{pmatrix})=
(a.c+0\sqrt[]{2}).(0+c.d\sqrt[]{2})](/latexrender/pictures/1658604b6482546912cf38039df47d01.png)
![=a.b.c.d\sqrt[]{2} =a.b.c.d\sqrt[]{2}](/latexrender/pictures/5b0b61fbcc619c3290e7077fbeef575c.png)
![=p\sqrt[]{2},p\in Z =p\sqrt[]{2},p\in Z](/latexrender/pictures/ffc081b4c4221c7583ff09ce8539ff63.png)
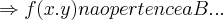
,logo A nao e isomorfo a B
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Dez 06, 2014 12:37
por adauto martins » Sáb Dez 06, 2014 12:37
uma correçao ....
![f(
\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=a.c+d.b\sqrt[]{2} f(
\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=a.c+d.b\sqrt[]{2}](/latexrender/pictures/ac3e11bb3d004049e562a0e65f0c6764.png)
![\neq f(
\begin{pmatrix} a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & b.d
\end{pmatrix})=(a.c+0\sqrt[]{2}).(0+b.d\sqrt[]{2})=a.b.c.d\sqrt[]{2}=p\sqrt[]{2} \neq f(
\begin{pmatrix} a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & b.d
\end{pmatrix})=(a.c+0\sqrt[]{2}).(0+b.d\sqrt[]{2})=a.b.c.d\sqrt[]{2}=p\sqrt[]{2}](/latexrender/pictures/8c52457c27c0976dfe29b5e84932199c.png)
logo nao satisfaz a propriedade multiplicativa de homomorfismos de A em B...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [triangulo] Duvida em um Desafio
por Gilder » Ter Fev 03, 2009 23:33
- 0 Respostas
- 821 Exibições
- Última mensagem por Gilder

Ter Fev 03, 2009 23:33
Geometria Plana
-
- [Quadrado] Duvida quanto a um desafio
por Gilder » Sex Jan 30, 2009 18:12
- 3 Respostas
- 3326 Exibições
- Última mensagem por Sandra Piedade

Ter Fev 03, 2009 08:32
Geometria Plana
-
- [Dúvida]Um desafio que envolve probabilidade
por Gabi Biel » Qui Out 17, 2013 20:37
- 5 Respostas
- 3826 Exibições
- Última mensagem por temujin

Sáb Out 19, 2013 21:05
Probabilidade
-
- Desafio
por Guarinense » Sex Nov 10, 2017 22:25
- 0 Respostas
- 5652 Exibições
- Última mensagem por Guarinense

Sex Nov 10, 2017 22:25
Teoria dos Números
-
- Desafio dos Dez Pontos
 por Molina » Sáb Jul 12, 2008 00:02
por Molina » Sáb Jul 12, 2008 00:02
- 6 Respostas
- 5299 Exibições
- Última mensagem por admin

Dom Jul 13, 2008 17:00
Desafios Fáceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
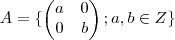
![B = Z[\sqrt[]{2}] = \{ a + b\sqrt[]{2} ; a,b \in Z\} B = Z[\sqrt[]{2}] = \{ a + b\sqrt[]{2} ; a,b \in Z\}](/latexrender/pictures/5dc859b87cd069ea4fd87390c50b3fbe.png)
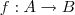 e mostrar que
e mostrar que 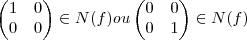 .
.
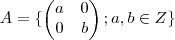
![B = Z[\sqrt[]{2}] = \{ a + b\sqrt[]{2} ; a,b \in Z\} B = Z[\sqrt[]{2}] = \{ a + b\sqrt[]{2} ; a,b \in Z\}](/latexrender/pictures/5dc859b87cd069ea4fd87390c50b3fbe.png)
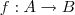 e mostrar que
e mostrar que 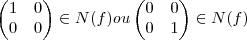 .
.
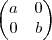
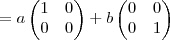 ,
,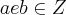 }
} seja um homomorfismo,f(x)=y,onde
seja um homomorfismo,f(x)=y,onde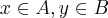 ...logo teremos
...logo teremos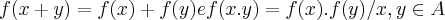
![(\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
c & 0 \\
0 & d
\end{pmatrix})=f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & c.d
\end{pmatrix})=
(a.c+0\sqrt[]{2}).(0+c.d\sqrt[]{2}) (\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
c & 0 \\
0 & d
\end{pmatrix})=f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & c.d
\end{pmatrix})=
(a.c+0\sqrt[]{2}).(0+c.d\sqrt[]{2})](/latexrender/pictures/1658604b6482546912cf38039df47d01.png)
![=a.b.c.d\sqrt[]{2} =a.b.c.d\sqrt[]{2}](/latexrender/pictures/5b0b61fbcc619c3290e7077fbeef575c.png)
![=p\sqrt[]{2},p\in Z =p\sqrt[]{2},p\in Z](/latexrender/pictures/ffc081b4c4221c7583ff09ce8539ff63.png)
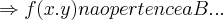 ,logo A nao e isomorfo a B
,logo A nao e isomorfo a B
![f(
\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=a.c+d.b\sqrt[]{2} f(
\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix}
.\begin{pmatrix}
a & 0 \\
0 & b
\end{pmatrix})=
f(\begin{pmatrix}
a.c & 0 \\
0 & b.d
\end{pmatrix})=a.c+d.b\sqrt[]{2}](/latexrender/pictures/ac3e11bb3d004049e562a0e65f0c6764.png)
![\neq f(
\begin{pmatrix} a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & b.d
\end{pmatrix})=(a.c+0\sqrt[]{2}).(0+b.d\sqrt[]{2})=a.b.c.d\sqrt[]{2}=p\sqrt[]{2} \neq f(
\begin{pmatrix} a.c & 0 \\
0 & 0
\end{pmatrix}).f(\begin{pmatrix}
0 & 0 \\
0 & b.d
\end{pmatrix})=(a.c+0\sqrt[]{2}).(0+b.d\sqrt[]{2})=a.b.c.d\sqrt[]{2}=p\sqrt[]{2}](/latexrender/pictures/8c52457c27c0976dfe29b5e84932199c.png) logo nao satisfaz a propriedade multiplicativa de homomorfismos de A em B...obrigado
logo nao satisfaz a propriedade multiplicativa de homomorfismos de A em B...obrigado


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.