Vestibulinho.
Não consigo resolver na teoria.
Existem 2 torneiras, para encher um tanque vazio. se apenas a primeira fosse aberta por completo,levaria 24 hrs. para encher um tanque.
E se apenas a segunda fosse aberta por completo levaria 48 hrs. para encher o mesmo tanque.
Se eu abrisse as duas juntas....... quanto tempo levaria para encher o tanque?
A)12
B)30
C)20
D)24
*E)16


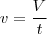
 é a vazão e
é a vazão e  o volume preenchido no tempo
o volume preenchido no tempo  .
.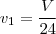 e
e 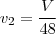 .
. . Assim,
. Assim, 
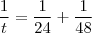
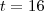 .
.

 .
.
 :
: