"Verificar se o subconjunto de P4 (R) é LI ou LD:
W= {x(x-1), x³, 2x³-x², x}"
Eu tentei resolver da seguinte forma:
>
 1*(x²-x) +
1*(x²-x) +  2*(x³) +
2*(x³) +  3*(2x³-x²) +
3*(2x³-x²) +  4*(x)
4*(x)> (-
 1 +
1 +  4)*x + (
4)*x + (  1 -
1 -  3)*x² + (
3)*x² + (  2 + 2*
2 + 2* 3)*x³
3)*x³|
 1 +
1 +  4 =0
4 =0|
 1 -
1 -  3 =0
3 =0|
 2 + 2*
2 + 2* 3 =0
3 =0Depois daí eu não consigo mais resolver, porque esse sistema não tem solução! :/
também não sei se fiz certo até aí,
por favor ajudem!

Obrigada.


 .
. 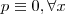 ,então
,então 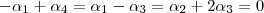 que é um sistema de três equações com 4 incógnitas , como o número de varáveis é maior que o de eq. é natural esperar que teremos algumas incógnitas em funções de outras . Por exemplo , escolhendo
que é um sistema de três equações com 4 incógnitas , como o número de varáveis é maior que o de eq. é natural esperar que teremos algumas incógnitas em funções de outras . Por exemplo , escolhendo 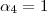 ,obteremos
,obteremos  e
e  .
.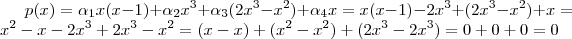
 .
.

 .
.
 :
: