Eu sei as operações básicas:adição,subtração,divisão,potenciação,radiciação e etc.O problema é que eu não consigo aplicar isso nas expressões algébricas!
Por exemplo,em:
Eu não sei resolver porque não sei como isolar o t...Ele está elevado a um número e está negativo,deveria passa-lo para o outro lado como? Multiplicando? Dividindo? Sem fazer nada?
E o pior é que eu não acho nenhum material que explique isso,deve ser um negócio muito básico mesmo,estou me sentindo um retardado!
Outro exemplo de expressão é:
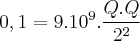
Eu não sei resolver esse tipo de coisa,na resolução o cara fez:
Eu entendi quando ele tirou a raiz,mas não entendi porque o 4 que era denominador do Q² virou numerador do 9!
Enfim,meu problema na maior parte são essas expressões elevadas a algo e que envolvem soma,adição,potência e etc,não sei qual operação prevalece.
Se puderem me ajudar,mesmo me mandando um link com esse tipo de expressão resolvida vocês estarão contribuindo muito,sério mesmo!
Obrigado!
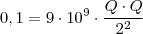
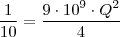
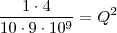
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.