por Gustavo Gomes » Ter Nov 12, 2013 19:38
Olá, pessoal.
Na questão:
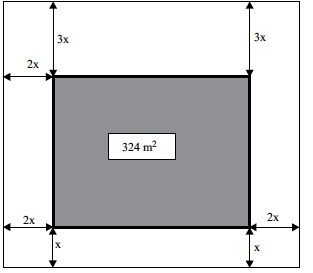
Em um terreno retangular, de 576 m², será construída uma horta que possuirá forma quadrada, de área 324 m². Em torno dessa horta, haverá uma calçada para circulação das pessoas, conforme representa a figura.
Determine a equação que permite calcular a distância x indicada na figura.
A resposta é 4x2 + 36x ? 63 = 0.
Grato.
- imagem.PNG (5.52 KiB) Exibido 932 vezes
-
Gustavo Gomes
- Usuário Parceiro
-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uma instituição tem seu terreno retangular limitado...
por ativirginis » Qui Fev 23, 2012 13:24
- 1 Respostas
- 1445 Exibições
- Última mensagem por timoteo
Qui Fev 23, 2012 15:43
Funções
-
- funções - área do terreno x valor
por rodrigo_sampaio » Seg Mai 19, 2014 16:58
- 0 Respostas
- 864 Exibições
- Última mensagem por rodrigo_sampaio
Seg Mai 19, 2014 16:58
Funções
-
- paralelepipedo retangular
por pedro martins » Sáb Jun 02, 2012 15:37
- 0 Respostas
- 1550 Exibições
- Última mensagem por pedro martins
Sáb Jun 02, 2012 15:37
Geometria Espacial
-
- Volume de uma caixa retangular
por Andreza » Sáb Nov 12, 2011 10:02
- 1 Respostas
- 1773 Exibições
- Última mensagem por LuizAquino
Qui Nov 17, 2011 22:16
Geometria Espacial
-
- Preço de um terreno
por Andreza » Ter Jan 17, 2012 16:20
- 1 Respostas
- 1251 Exibições
- Última mensagem por MarceloFantini
Ter Jan 17, 2012 19:17
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é
.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01
Como
:
O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
