 por raimundoocjr » Qui Mai 30, 2013 22:59
por raimundoocjr » Qui Mai 30, 2013 22:59
Calcular
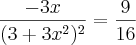
.
-
raimundoocjr
-
 por e8group » Sex Mai 31, 2013 11:27
por e8group » Sex Mai 31, 2013 11:27
Esta equação não admite solução real .De fato : Reescrevemos
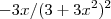
como
![-x/[3(x^2+1)^2] -x/[3(x^2+1)^2]](/latexrender/pictures/4c6f0a02d5740fcaf4becb907a397f8a.png)
e considerando este resultado uma função

.Observando que o denominador é sempre positivo para quaisquer

real ,então comparando a igualdade dada (equação) é fácil ver que se

admite um número finito de soluções reais ,então obrigatoriamente tais soluções são

,mas isto contradiz o teorema do valor intermediário (TVI) , pois

é contínua em

e
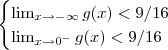
o que implica que não existe

em quaisquer intervalos
![[M,N] \subset (-\infty,0) [M,N] \subset (-\infty,0)](/latexrender/pictures/af2eb4470c1b5710264ebcc15f00d687.png)
(ou
![[N,M] \subset (-\infty,0) ) [N,M] \subset (-\infty,0) )](/latexrender/pictures/f4f0100c56e6c0a8d17ddab86d7e0c76.png)
tais que

.Logo pelo (TVI), concluímos que a suposição de

admite um número finito de soluções reais é falsa ,i.e,a equação não admite solução real .
Outra forma que achei interessante :
Usando que necessariamente
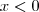
,fazendo a substituição trigonométrica
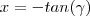
para
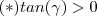
,temos :
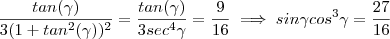
.Esta igualdade é uma contradição .Pois
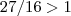
e as funções seno e cosseno são limitadas , pela hipótese

tem-se
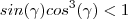
.Absurdo ! .
A primeira solução acho que ela é aceita ,a segunda talvez ela seja .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por raimundoocjr » Sex Mai 31, 2013 15:34
por raimundoocjr » Sex Mai 31, 2013 15:34
Entendi. Valeu!
-
raimundoocjr
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7467 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3212 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2748 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2713 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2654 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
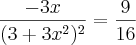 .
.

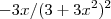 como
como ![-x/[3(x^2+1)^2] -x/[3(x^2+1)^2]](/latexrender/pictures/4c6f0a02d5740fcaf4becb907a397f8a.png) e considerando este resultado uma função
e considerando este resultado uma função  .Observando que o denominador é sempre positivo para quaisquer
.Observando que o denominador é sempre positivo para quaisquer  real ,então comparando a igualdade dada (equação) é fácil ver que se
real ,então comparando a igualdade dada (equação) é fácil ver que se  admite um número finito de soluções reais ,então obrigatoriamente tais soluções são
admite um número finito de soluções reais ,então obrigatoriamente tais soluções são  ,mas isto contradiz o teorema do valor intermediário (TVI) , pois
,mas isto contradiz o teorema do valor intermediário (TVI) , pois  é contínua em
é contínua em  e
e 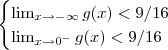 o que implica que não existe
o que implica que não existe  em quaisquer intervalos
em quaisquer intervalos ![[M,N] \subset (-\infty,0) [M,N] \subset (-\infty,0)](/latexrender/pictures/af2eb4470c1b5710264ebcc15f00d687.png) (ou
(ou ![[N,M] \subset (-\infty,0) ) [N,M] \subset (-\infty,0) )](/latexrender/pictures/f4f0100c56e6c0a8d17ddab86d7e0c76.png) tais que
tais que  .Logo pelo (TVI), concluímos que a suposição de
.Logo pelo (TVI), concluímos que a suposição de  admite um número finito de soluções reais é falsa ,i.e,a equação não admite solução real .
admite um número finito de soluções reais é falsa ,i.e,a equação não admite solução real .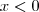 ,fazendo a substituição trigonométrica
,fazendo a substituição trigonométrica 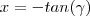 para
para 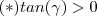 ,temos :
,temos : 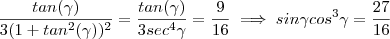 .Esta igualdade é uma contradição .Pois
.Esta igualdade é uma contradição .Pois 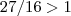 e as funções seno e cosseno são limitadas , pela hipótese
e as funções seno e cosseno são limitadas , pela hipótese tem-se
tem-se 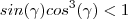 .Absurdo ! .
.Absurdo ! .





