 por Jhenrique » Seg Dez 10, 2012 18:29
por Jhenrique » Seg Dez 10, 2012 18:29
Olá,
Sabemos que num triângulo retângulo é verdadeiro que a soma das áreas dos catetos é igual a área da hipotenusa.
Isto é:

Agora, adicionando o conceito de unidade a esta fórmula, como ficaria?
Assim?
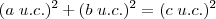
sendo:
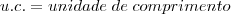
Ou assim?

Sendo:
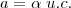
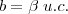

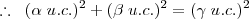
Bem, o que eu busco saber com essa pergunta!? Em 1º lugar, buscar um padrão para as situações semelhantes, é isso o que fazemos em ciencias exatas, buscamos regras gerais e padrões, e em 2º lugar, na álgebra, existe um elemento para representar uma grandeza, um elemento para representar uma unidade e um elemento para representar o coeficiente desta unidade, então, quero fazer um cara-crachá nas fórmulas matemáticas.
Grato!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por delara » Sáb Fev 02, 2013 14:48
por delara » Sáb Fev 02, 2013 14:48
Creio que há um equívoco na sua afirmação:
Sabemos que num triângulo retângulo é verdadeiro que a soma das áreas dos catetos é igual a área da hipotenusa.
O Teorema de Pitágoras pode relacionar tanto comprimentos como áreas. Portanto o correto seria:
Sabemos que num triângulo retângulo é verdadeiro que a soma
dos comprimentos dos quadrados dos catetos é igual ao quadrado
do comprimento da hipotenusa.
Ou
Sabemos que num triângulo retângulo é verdadeiro que a soma
das áreas dos quadrados cujos lados são catetos é igual
a área do quadrado cujo lado é a hipotenusa.
Mas não consegui entender muito bem a sua dúvida, creio que as duas formas representadas estão corretas.
Pois tendo o Teorema de Pitágoras:

As unidades de

são em COMPRIMENTO, ou seja, a = 10cm, a = 20dm, a = 10m, a = 12km, etc.
As unidades de

também estão em comprimento,

= 10cm,

= 20dm,

= 10m,

= 12km, etc.
Implicitamente, as duas formas que você apresentou são a mesma coisa.
-
delara
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jan 31, 2013 09:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas/Engenharia
- Andamento: cursando
 por Russman » Sáb Fev 02, 2013 18:16
por Russman » Sáb Fev 02, 2013 18:16
Quanto a sua afirmação sobre o teorema de pitágoras o amigo ali de cima está correto. Cuidado com as palavras! Se você se preocupa tanto com formalidades é interessante observar bem as afirmações.
Quanto as unidades eu acredito que você está confundindo a economia de notação com a inexistência de dimensão. Existem grandezas que são adimensionais e não é necessário adotar uma unidade para medi-las, como os ângulos por exemplo. No caso do Teorema nós apenas não escrevemos unidade juntamente na fórmula por uma questão de economia de notação e/ou por estar explicito que os termos

,

e

são grandezas de comprimento. Você decide como expor a unidade da grandeza!
E

[L].
Usamos [L] para generalizar as unidades de comprimento.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Dom Fev 03, 2013 01:04
por Jhenrique » Dom Fev 03, 2013 01:04
Eu já obtive a resposta que buscava...
pelo menos a conclusão que cheguei foi esta:
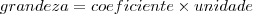
no teorema de pitágoras (

) ,

,

e

são
grandezas.
Ter entendido isso de modo explícito para mim foi importante, no entanto, a cada coisa que eu entendo implica em mais duas coisas novas que ainda não entendo... afff
de qualquer forma... obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ÁLGEBRA EM FÓRMULAS]
por Andreyan » Qui Ago 16, 2012 14:09
- 4 Respostas
- 3064 Exibições
- Última mensagem por Russman

Sex Ago 17, 2012 16:15
Cálculo: Limites, Derivadas e Integrais
-
- [Editor de Fórmulas]
por dehcalegari » Ter Ago 27, 2013 11:49
- 1 Respostas
- 1406 Exibições
- Última mensagem por Cleyson007

Ter Ago 27, 2013 11:54
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração de fórmulas de derivadas
por victoreis1 » Qua Nov 24, 2010 20:09
- 1 Respostas
- 3064 Exibições
- Última mensagem por MarceloFantini

Qui Nov 25, 2010 00:43
Cálculo: Limites, Derivadas e Integrais
-
- Relação entre duas fórmulas
por FelipeScheidemantel » Qui Mar 19, 2009 19:19
- 0 Respostas
- 1759 Exibições
- Última mensagem por FelipeScheidemantel

Qui Mar 19, 2009 19:19
Álgebra Elementar
-
- Ajuda com fórmulas de crescimento econômico
por RChaves » Dom Nov 15, 2009 00:26
- 0 Respostas
- 1539 Exibições
- Última mensagem por RChaves

Dom Nov 15, 2009 00:26
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

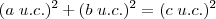 sendo:
sendo: 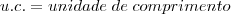

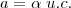
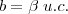

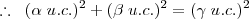



 são em COMPRIMENTO, ou seja, a = 10cm, a = 20dm, a = 10m, a = 12km, etc.
são em COMPRIMENTO, ou seja, a = 10cm, a = 20dm, a = 10m, a = 12km, etc.  também estão em comprimento,
também estão em comprimento, 
 e
e  são grandezas de comprimento. Você decide como expor a unidade da grandeza!
são grandezas de comprimento. Você decide como expor a unidade da grandeza!  [L].
[L].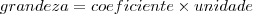


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.