 por JOHNY » Qui Set 02, 2010 18:31
por JOHNY » Qui Set 02, 2010 18:31
QUATRO CORREDORES, JOAO, PEDRO, ANDRE E FABIO COMBINARAM QUE, AO FINAL DE CADA CORRIDA, O QUE FICASSE EM ULTIMO LUGAR DOBRARIA O DINHEIRO QUE CADA UM DOS OUTROS POSSUIA. COMPETIRAM 4 VEZES E FICARAM EM ULTIMO LUGAR NA PRIMEIRA, SEGUNDA, TERCEIRA E QUARTA CORRIDAS RESPECTIVAMENTE, JOAO, PEDRO, ANDRE E FABIO. SE NO FINAL DA QUARTA COMPETICAO, CADA UM FICOU COM 16 REAIS, ENTAO INICIALMENTE JOAO POSSUIA????
-
JOHNY
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Set 02, 2010 18:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por alexandre32100 » Sex Set 03, 2010 16:14
por alexandre32100 » Sex Set 03, 2010 16:14
É só fazer o caminho inverso:
No final, todos tinha

reais e Fábio perdeu a última corrida. Quer dizer que, antes dela, João, Pedro e André tinham
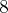
reais cada e Fábio

reais.
André perdeu a 3ª corrida. Antes dela, João e Pedro tinham

reais cada, Fábio tinha
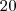
reais e André
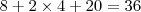
reais, continuando o raciocínio, chegará ao resultado desejado...
-
alexandre32100
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10722 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9734 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3317 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4615 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6538 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 reais e Fábio perdeu a última corrida. Quer dizer que, antes dela, João, Pedro e André tinham
reais e Fábio perdeu a última corrida. Quer dizer que, antes dela, João, Pedro e André tinham 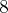 reais cada e Fábio
reais cada e Fábio  reais.
reais. reais cada, Fábio tinha
reais cada, Fábio tinha 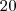 reais e André
reais e André 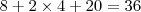 reais, continuando o raciocínio, chegará ao resultado desejado...
reais, continuando o raciocínio, chegará ao resultado desejado...