Os lados de um triângulo retângulo estão em PA de razão r. Para este triângulo, a distância entre o incentro e o circuncentro é:
a)rV5/2
b)rV3/2
c)rV2/2
d)r
e)r/2



 .
.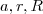 as medidas do menor lado do triângulo(No desenho
as medidas do menor lado do triângulo(No desenho 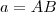 ), a razão da progressão e o raio da circunferência inscrita no triângulo, respectivamente, temos:
), a razão da progressão e o raio da circunferência inscrita no triângulo, respectivamente, temos:
 . Tracando também segmentos do centro para os vértices não retos, da congruência dos triângulos podemos fazer:
. Tracando também segmentos do centro para os vértices não retos, da congruência dos triângulos podemos fazer: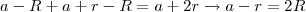 e assim as coordenadas do incentro são :
e assim as coordenadas do incentro são : 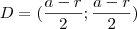
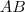 é uma reta paralela ao lado
é uma reta paralela ao lado  , portanto paralela ao eixo
, portanto paralela ao eixo 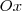 . Assim, terá equação
. Assim, terá equação  . Já a reta mediatriz do outro cateto será paralela ao cateto que mede
. Já a reta mediatriz do outro cateto será paralela ao cateto que mede  , isto é, será uma reta perpendicular ao eixo
, isto é, será uma reta perpendicular ao eixo 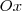 , portanto de equação:
, portanto de equação: 

 e o circuncentro
e o circuncentro 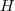 será:
será:![d=\sqrt{[\frac{a-r}{2}-(\frac{a+r}{2})]^2+(\frac{a-r}{2}-\frac{a}{2})^2}=\sqrt{r^2+\frac{r^2}{4}}=\sqrt{\frac{5r^2}{4}}=\frac{r\sqrt{5}}{2} d=\sqrt{[\frac{a-r}{2}-(\frac{a+r}{2})]^2+(\frac{a-r}{2}-\frac{a}{2})^2}=\sqrt{r^2+\frac{r^2}{4}}=\sqrt{\frac{5r^2}{4}}=\frac{r\sqrt{5}}{2}](/latexrender/pictures/ff9c05193dd689dffc3886ae337052a5.png)

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

