é o seguinte:
sabemos que o cociente de dois numeros irracionais pode ser um numero racional. Das alternativas abaixo, qual exemplifica essa afirmação?
a)
![\frac{\sqrt[]{2}}{\sqrt[]{4}}](/latexrender/pictures/7164a9a9b857fd1c37bc40472aa70b46.png "\frac{\sqrt[]{2}}{\sqrt[]{4}}")
= ![\frac{1}{\sqrt[]{2}}](/latexrender/pictures/a708a9a9173a86197e94e74a716f2bea.png "\frac{1}{\sqrt[]{2}}")
b)
![\frac{\sqrt[]{2}}{\sqrt[]{18}}](/latexrender/pictures/dfa194d9e2fe78cf1c7d6984df16a7bd.png "\frac{\sqrt[]{2}}{\sqrt[]{18}}")
= ![\frac{1}{\sqrt[]{9}}](/latexrender/pictures/b3db8d58f558413c5f5cafa466991c47.png "\frac{1}{\sqrt[]{9}}")
porque a letra a nao vai resultar tambem num numero racional???
fiz meios por extremos e as duas alternativas deu 1 porque a letra a nao é racional
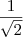não é racional. Já 
, logo racional.
![\sqrt[2]{2} / \sqrt[2]{18} = 1 / \sqrt[2]{9}](/latexrender/pictures/028f397ba376a7e42a7fa60b210bf989.png "\sqrt[2]{2} / \sqrt[2]{18} = 1 / \sqrt[2]{9}")
?
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)